Materi tentang Barisan Aritmetika Kelas 10 Fase E, rumus suku ke-n contoh soalnya dibahas lengkap di artikel ini!
Barisan Aritmetika ada juga yang menyebut barisan aritmatika membahas khusus tentang kumpulan suatu bilangan yang memiliki pola tertentu. Adapun materi yang akan kita pelajari pada barisan aritmetika adalah barisan, sisipan dan suku tengah barisan aritmatika. Selain barisan aritmetika, juga akan dibahas tentang barisan geometri, deret aritmatika, dan deret geometri, silahkan dibaca pada artikel.
Barisan Bilangan
Perhatikan pola bilangan: 4, 6, 8, 10, ….
Jika diamati lebih teliti, pola bilangan di atas disusun berdasarkan aturan tertentu.
Pola bilangan yang demikian disebut dengan barisan bilangan.
Pengertian Barisan
Barisan merupakan kumpulan suatu bilangan (atau bentuk aljabar) yang disusun sehingga membentuk suku-suku yang dipisahkan dengan tanda koma dan memiliki pola tertentu. Bentuknya disusun sebagai berikut :
$$ u_1, u_2, u_3, u_4, u_5, u_6, u_7, …. $$
Keterangan :
$ u_1 $ artinya suku ke-1 (suku pertama)
$ u_2 $ artinya suku ke-2 (suku kedua)
dan seterusnya….
Contoh : Berikut beberapa contoh barisan!
- Barisan bilangan ganjil : 1, 3, 5, 7, ….
Keterangan :
suku ke-1 (suku pertama) adalah 1 ($u_1 = 1$),
suku ke-2 (suku kedua) adalah 3 ($u_2=3$),
suku ke-3 (suku ketiga) adalah 5 ($u_3=5$),
dan seterusnya …. - Barisan bilangan genap : 2, 4, 6, 8, ….
- Barisan sebarang : 1, 5, 3, -2, 5, 7, …
Barisan Aritmetika
Suatu barisan dengan beda atau selisih antara dua suku berurutan selalu tetap atau konstan disebut BARISAN ARITMETIKA. Beda pada barisan aritmetika dilambangkan dengan $b$.
Misal barisannya : $ u_1, u_2, u_3, u_4, u_5, u_6, u_7, …. $
Cara menghitung bedanya ($b$) adalah
$ b = u_2 - u_1 $
$ b = u_3 - u_2 $
$ b = u_4 - u_3 $
.
.
.
$b = u_n - u_{n-1} $
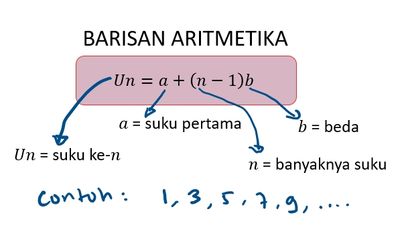
Adapun rumus suku ke-$n$ nya adalah $ u_n = a + (n-1)b $
dengan $ a $ = suku pertamanya ($u_1$), $ b $ = bedanya, dan $ u_n $ = suku ke-$n$
Dari rumus suku ke-$n$ nya, dapat disusun barisan aritmetikanya,
$ u_n = a + (n-1)b $
$ u_1 = a + (1-1)b = a $
$ u_2 = a + (2-1)b = a + b $
$ u_3 = a + (3-1)b = a + 2b $
$ u_4 = a + (4-1)b = a + 3b $
$ u_5 = a + (5-1)b = a + 4b $
dan seterusnya …..
sehingga barisan aritmetikanya : $ a, a+b, a+2b, a+3b, …. $
Contoh:
Tentukan suku ke-101 dari barisan aritmetika -1, 3, 7, 11, 15, ….?
Penyelesaian :- dari barisannya diperoleh $ a = -1 $ dan $ b = 7-3 = 4 $
- Menentukan suku ke-101 dengan $ u_n = a + (n-1)b $
$ u_{101} = a + (101-1)b = -1 + 100 \times 4 = -1 + 400 = 399 $
Jadi, suku ke-101 nya adalah 399 ($u_{101} = 399$).
Diketahui suku ke-3 dan suku ke-6 suatu barisan aritmetika berturut-turut 9 dan 18. Tentukan nilai suku ke-11 dan rumus suku ke-n nya!
Penyelesaian :- Diketahui $ u_3 = 9 $ dan $ u_6 = 18 $
Untuk menentukan nilai suku pada suatu barisan, kita memerlukan nilai $ a $ dan bedanya ($b$) dengan menjabarkan suku-suku yang diketahui. - Rumus suku ke-$n : u_n = a+ (n-1)b $
$$ u_6 = a+(6-1)b \\ \rightarrow 18= a + 5b \\ \rightarrow a + 5b = 18 \text{…. pers(i)}$$
$$ u_3 = a+(3-1)b \\ \rightarrow 9= a + 2b \\ \rightarrow a + 2b = 9 \text{…. pers(ii)}$$ - Menentukan nilai $ a $ dan $ b $ dengan eliminasi pers(i) dan pers(ii)
$$ \begin{array}{cc}a + 5b = 18 & \\a + 2b = 9 &- \\\hline3b = 9 & \\b = 3 &\end{array} $$
Pers(ii) : $ a + 2b = 9 \rightarrow a + 2(3) = 9 \rightarrow a = 3 $ - Menentukan rumus suku ke-$n$
$$\begin{align*} u_n &= a+(n-1)b \\ u_n&= 3 + (n-1)3 \\u_n&= 3+3n-3 \\u_n&=3n \end{align*}$$
Jadi, rumus suku ke-$n$ nya adalah $U_n=3n$. - Menentukan suku ke-11
$ u_{11} = 3(11) = 33 $
Jadi, suku ke-11 nya adalah 33.
- Diketahui $ u_3 = 9 $ dan $ u_6 = 18 $
Seorang pegawai di BUMN mendapatkan gaji pada tahun 2020 sebesar 3,2 juta. Kemudian ia mendapatkan kenaikan gaji yang tetap setiap 2 tahun. Jika Pegawai tersebut mendapat gaji 4 Juta pada tahun 2028. Tentukan
- a. Berapa rupiah selisih nominal keniakan gaji setiap 2 tahun?
- b. Tentukan berapa rupiah gaji yang didapat pada tahun 2016?