Barisan Dan Deret Aritmetika, Rumus Dan Penerapannya

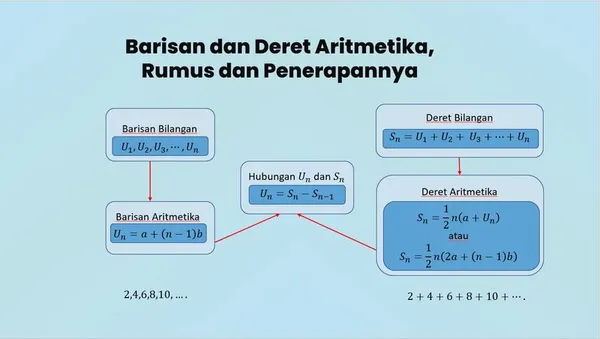
Pelajari konsep dasar barisan dan deret aritmetika matematika. Artikel ini menjelaskan apa itu barisan dan deret aritmetika, rumus, dan bagaimana penerapan dalam kehidupan sehari-hari.

Barisan dan deret aritmetika adalah dua konsep matematika yang penting dan sering digunakan dalam berbagai konteks. Pola barisan tentunya sudah kalian pelajari mulai dari jenjang SMP ya. Dalam artikel ini, kita akan menjelaskan pengertian, rumus, dan beberapa penerapan dari kedua konsep ini. Selain barisan dan deret aritmetika, juga akan dibahas tentang barisan dan deret geometri, silahkan dibaca pada artikel Barisan dan Deret Geometri↝ . Untuk lebih jelasnya, mari kita simak penjelasan masing-masing berikut ini.

1. Pengertian Barisan Bilangan

Barisan bilangan adalah urutan bilangan yang diatur dalam suatu pola tertentu atau urutan berdasarkan aturan tertentu. Barisan ini bisa terdiri dari bilangan bulat, bilangan riil, atau jenis bilangan lainnya dan biasanya dipisahkan dengan tanda koma. Setiap angka dalam barisan disebut suku barisan, dan setiap suku memiliki posisi dalam barisan yang menunjukkan urutannya.

Dalam barisan bilangan, aturan atau pola yang digunakan untuk menghasilkan setiap suku biasanya konsisten atau memiliki hubungan matematis tertentu antara suku-suku berurutan. Pola ini dapat berupa penambahan, pengurangan, perkalian, pembagian, atau hubungan matematis lainnya.

Contoh Barisan Bilangan

Berikut adalah beberapa contoh barisan bilangan dengan pola berbeda

a. 1, 2, 3, 4, 5,….
b. 2, 4, 6, 8, 10,….
c. 14, 11, 8, 5, 2,….
d. 2,– 2, 2, – 2, 2, – 2,….

Pada contoh diatas, bilangan-bilangan pada a,b,c,d,e mempunyai aturan tertentu sehingga disebut sebagai barisan bilangan.

a. $\underbrace{1, 2}_{+1} \underbrace{, 3 }_{+1} \underbrace{, 4 }_{+1} \underbrace{, 5 }_{+1} , ….$
b. $\underbrace{2, 4}_{+2} \underbrace{, 6 }_{+2} \underbrace{, 8 }_{+2} \underbrace{, 10 }_{+2} , ….$
c. $\underbrace{14, 11}_{-3} \underbrace{, 8 }_{-3} \underbrace{, 5 }_{-3} \underbrace{, 2 }_{-3} , ….$
d. $\underbrace{2, -2}_{-4} \underbrace{, 2 }_{+4} \underbrace{, -2 }_{-4} \underbrace{, 2 }_{+4} , ….$

Catatan

• Tiap-tiap bilangan pada barisan bilangan disebut suku (U)
• Suku pertama dilambangkan dengan $U_1$ atau $a$
• Suku kedua dilambangkan dengan $U_2$
• Suku ketiga dilambangkan dengan $U_3$
• Suku ke-n dilambangkan dengan $U_n$ dengan $n ∈ A$ (bilangan Asli)

2. Barisan Aritmetika

Barisan aritmetika adalah barisan bilangan yang selisih antara dua suku yang berurutan sama atau tetap.

Contoh :
a. 3, 8, 13, 18, ….
b. 10, 7, 4, 1, ….

Pada contoh diatas selisih antara dua suku berurutan tetap.

a. $\underbrace{3, 8}_{+5} \underbrace{, 13 }_{+5} \underbrace{, 18 }_{+5} \underbrace{, 5 }_{+1} , ….$
b. $\underbrace{10, 7}_{-3} \underbrace{, 4 }_{-3} \underbrace{, 1 }_{-3} \underbrace{, 10 }_{+2} , ….$

Selisih dua suku yang berurutan disebut beda atau disimbolkan dengan huruf $b$.

Untuk menentukan beda digunakan Rumus :

$b = U_2 - U_1$
$b = U_3 - U_2$
$b = U_4 - U_3$
.
.
.
$b = U_n - U_{n-1}$

Jika suku pertama = $a$ dan beda = $b$, maka secara umum barisan Aritmetika tersebut adalah: $$\begin{matrix}U_1, & U_2, & U_3, & U_4, & & U_n \\ a, & a+b, & a+2b, & a+3b, & \cdots, &a+(n-1)b \end{matrix}$$

Jadi rumus suku ke-n barisan aritmetika adalah $$U_n=a+(n-1)b$$ Dengan :
$U_n$ = Suku ke-n
$a$ = Suku pertama
$b$ = beda atau selisih

Contoh Soal Barisan Aritmetika

1. Dari barisan $3, 5, 7, 9, 11, \cdots$ suku ke-$21$ adalah…

   Alternatif Penyelesaian ✍️

   Dari barisan $3, 5, 7, 9, 11, \cdots$ kita peroleh
   suku pertama $a=3$ dan
   beda $b=5-3=2$ atau $b=11-9=2$.

   Suku ke-$21$ adalah: $$\begin{align*} U_{n} &= a+\left( n-1 \right)b \\ U_{21} &= 3+\left( 21-1 \right)(2) \\ &= 3+\left( 20 \right)(2) \\ &= 3+40 =43 \end{align*}$$

   $\therefore$ Jadi, suku ke-$21$ dari barisan $3, 5, 7, 9, 11, \cdots$ adalah $43$

2. Suatu barisan aritmatika diketahui suku ke-$6$ adalah $-4$ dan suku ke-$9$ adalah $-19$, maka tentukan suku ke-$11$!

   Alternatif Penyelesaian ✍️

   Diketahui :
   $𝑈_{6} = -4$
   $𝑈_{9} = -19$
   **Ditanyakan :** $𝑈_{11} = \cdots ?$
   **Jawab:**
   Rumus suku ke-$n$ adalah $U_{n} = a+\left( n-1 \right)b$, kita peroleh: $$\begin{align*} U_{6} &= -4 & \text{}\\ a+5b &= -4 & \cdots\text{pers (1)}\\ U_{9} &= -19 & \text{}\\ a+8b &= -19 & \cdots\text{pers (2)}\\ \end{align*}$$

   Dari kedua persamaan di atas kita peroleh:

   • cari nilai b
     $$\begin{align*} a+5b &= -4 \\ a+8b &= -19\ (-)\\ \hline -3b= 15 \\ b= -5 \end{align*}$$
   • substitusi $b=-5$ ke pers (1)
     $$\begin{align*} a+5b &= -4 \\ a+8(-5) &= -19\\ a-40 &= -19\\ a &= 21 \end{align*}$$
   • cari $U_{11}$
     $$\begin{align*} U_{11}= a+10b \\ &= 21+10(-5) \\ &= 21-50=-29 \end{align*}$$

   $\therefore$ Jadi, suku ke-11 adalah -29.

Logika Praktis
Beda adalah suku besar kurangi suku kecil, lalu hasilnya dibagi dengan selisih indeks suku besar dikurangi indeks suku kecil. $$b=\frac{U_q-U_p}{q-p}$$

Contoh

Jika diketahui $𝑈_3 = 24$ dan $𝑈_8 = 54$, tentukan suku ke-15 dari barisan tersebut!

Langkah logika praktis:
Suku ke 15 adalah suku ke-8 ditambah 7 beda. Jadi, $$\begin{align*}𝑈_{15} &= 𝑈_8 + 7𝑏\\&= 54 + 7 \left( \frac{54−24}{8−3} \right)\\&= 54 + 7(6)\\&= 54 + 42\\&= 96\end{align*}$$

3. Deret Aritmetika

Deret Aritmetika adalah jumlah dari seluruh suku-suku pada barisan aritmetika.

Jika barisan aritmetikanya adalah $U_1, U_2, U_3, \cdots, U_n$ maka
deret aritmetikanya $U_1+U_2+ U_3+ \cdots+ U_n$ dan
dilambangkan dengan $S_n$.

Rumus Jumlah n Suku Pertama Deret Aritmetika $$S_n=\frac12n(a+U_n)$$ atau $$S_n=\frac12n(2a+(n-1)b)$$

dengan:
$S_n$ = Jumlah n suku pertama deret aritmetika
$U_n$ = Suku ke-n deret aritmetika
$a$ = suku pertama
$b$ = beda
$n$ = banyaknya suku

Contoh Soal Deret Aritmetika

1. Tentukan jumlah 20 suku pertama deret aritmetika 3+7+11+…

   Alternatif Penyelesaian ✍️

   Dari deret 3+7+11+… kita peroleh
   $a=3 \\ b=7-3=4$

   selanjutnya substitusi ke dalam rumus $S_n$

   $$\begin{align*}S_n&=\frac12n(2a+(n-1)b)\\ S_{20}&=\frac12{20}(2(3)+(20-1)4)\\ S_{20}&=10(6+19(4))\\ S_{20}&=10(6+76)\\S_{20}&=10(82)\\ S_{20}&=820\\ \end{align*}$$

   Jadi, jumlah 20 suku pertamanya adalah 820.

2. Tentukan hasil dari $5 + 7 + 9 + 11 + \cdots + 41$ !

   Alternatif Penyelesaian ✍️

   Dari bentuk $5 + 7 + 9 + 11 + \cdots + 41$ diketahui merupakan deret aritmetika sehingga
   $a=5\\b=2\\U_n=41$
   • selanjutnya cari banyaknya suku (n) $$\begin{align*} U_{n}= a+\left( n-1 \right)b \\ 41 &= 5+\left( n-1 \right)(2) \\ 41 &= 5+ 2n-2 \\ 38 &= 2n\\ n &= 19 \end{align*}$$
   • substitusi $n=19$ ke $S_n$ untuk mencari jumlah n suku pertama $$\begin{align*} S_{n}&= \dfrac{n}{2} \left( a+U_{n} \right) \\ S_{19}&= \dfrac{19}{2} \left( 5+ 41 \right) \\ &= \dfrac{19}{2} \left( 46 \right) \\ &= 23 \times 19 = 437 \end{align*}$$

   Jadi, hasil dari $5 + 7 + 9 + 11 + \cdots + 41=437.$

3. Tentukan jumlah semua bilangan ganjil antara 10 dan 200 !

   Alternatif Penyelesaian ✍️

   Jumlah bilangan ganjil antara 10 dan 200 dapat dituliskan dalam deret sebagai berikut $$11 + 13 + 15 + 17 + \cdots +199$$ Deret di atas membentuk deret aritmetika dengan $a=11\\b=2\\U_n=199$
   • selanjutnya cari banyaknya suku (n) $$\begin{align*} U_{n}&= a+\left( n-1 \right)b \\ 199 &= 11+\left( n-1 \right)(2) \\ 199 &= 11+ 2n-2 \\ 190 &= 2n\\ n &= 95 \end{align*}$$
   • substitusi $n=95$ ke $S_n$ untuk mencari jumlah n suku pertama $$\begin{align*} S_{n}&= \dfrac{n}{2} \left( a+U_{n} \right) \\ S_{95}&= \dfrac{95}{2} \left( 11+ 199 \right) \\ &= \dfrac{95}{2} \left( 210 \right) \\ &= 95 \times 105 = 9975 \end{align*}$$

Jadi, jumlah semua bilangan ganjil antara 10 dan 200 adalah 9975

4. Penerapan Barisan dan Deret Geometri

Berikut beberapa penerapan dari barisan dan deret geometri, sebenarnya masih banyak ya. matematika tidak lepas dari kehidupan dunia nyata.

1. Seorang pegawai di BUMN mendapatkan gaji pada tahun 2020 sebesar 3,2 juta. Kemudian ia mendapatkan kenaikan gaji yang tetap setiap 2 tahun. Jika Pegawai tersebut mendapat gaji 4 Juta pada tahun 2028. Tentukan

   • a. Berapa rupiah selisih nominal keniakan gaji setiap 2 tahun?
   • b. Tentukan berapa rupiah gaji yang didapat pada tahun 2016?

   Alternatif Penyelesaian ✍️

   Diketahui :

   gaji 2020 sebesar 3,2 Juta $\rightarrow U_1=3,2$
   kenaikan setiap 2 tahun sehingga pada tahun 2028 mengalami 4 kali kenaikan maka $n=4+1=5$
   gaji 2028 sebesar 4 Juta $\rightarrow U_5=4$

   Ditanya:

   • a. selisih gaji setiap 2 tahun $\rightarrow b=\cdots?$
   • b. gaji pada tahun 2016?

   Jawab

   • a. cari $b$ dengan rumus $U_n$ $$\begin{align*} b&=\frac{U_q-U_p}{q-p}\\b&=\frac{U_5-U_1}{5-1}\\b&=\frac{4-3,2}{5-1} \\ b&=\frac{0,8}{4}\\b&=0,2\text{ juta}\end{align*}$$ Jadi, selisih gaji setiap 2 tahun adalah 0,2 juta atau 200.000

   • b. gaji pada tahun 2016 sama dengan gaji 2020 dikurangi 2 kali kenaikan sehingga $$Gaji = U_1-2b=3,2-2(0,2)\\=3,2-0,4=2,8\text{ juta}$$

   Jadi, gaji pada tahun 2016 adalah 2,8 juta.

2. Soal UNBK Matematika IPA 2019
   Seorang peternak ayam petelur mencatat banyak telur yang dihasilkan selama $12$ hari. Setiap hari, banyaknya telur yang dihasilkan bertambah $4$ buah. Jika hari pertama telur yang dihasilkan berjumlah $20$ buah, jumlah seluruh telur selama $12$ hari adalah… (A) 480
   (B) 496
   (C) 504
   (D) 512
   (E) 520

   Alternatif Penyelesaian ✍️

   Pertambahan telur setiap hari adalah sama, ini sesuai dengan konsep deret aritmetika. Dengan suku pertama $a=20$ dan pertambahan $b=4$, maka deretnya adalah $20+24+28+\cdots$ dan jumlah $12$ suku pertama adalah: $$\begin{align*} S_{n} & = \dfrac{n}{2} \left(2a+(n-1)b \right) \\ S_{12} & = \dfrac{12}{2} \left(2(20)+(12-1)(4) \right) \\ & = 6 \left(40+44 \right) \\ & = 6 \left(84 \right) =504 \end{align*}$$

   $\therefore$ Pilihan yang sesuai adalah $(C) 504$

Demikian, materi Barisan dan deret Aritmetika. Banyak sekali soal-soal yang berkaitan dengan barisan dan deret aritmatika. Kalian bisa kembangkan sendiri ya..