Yuk belajar materi Fungsi Kuadrat Materi matematika Kelas X fase E kurikulum merdeka! Mulai dari Pengertian, bentuk umum, hingga Contoh Soal fungsi kuadrat. pelajari selengkapnya disini!

Daftar Isi

Sobat Sinmat, pernahkah kamu mengitung berapa tinggi puncak air mancur di suatu taman? yeay, kamu bisa menggunakan materi fungsi kuadrat lho untuk menghitungnya. Apa sih fungsi kuadrat dan kegunaannya? Fungsi kuadrat ini merupakan materi matematika yang kamu pelajari pada jenjang SMA/SMK kelas X atau kalau di kurikulum merdeka ada di fase E ya sob.

Dengan mempelajari fungsi kuadrat, kamu juga bisa menghitung puncak tertinggi dari jembatan lengkung, roket yang ditembakkan keatas dan lain sebagainya. yuk simak penjelasan lengkapnya berikut ini.

Pengertian Fungsi Kuadrat

Fungsi kuadrat adalah salah satu jenis dari fungsi polinomial dimana pangkat tertinggi variabelnya adalah dua. Lalu apa yang dimaksud dengan fungsi polinomial? jika terdapat pangkat bilangan bulat nonnegatif $n$ dan bilangan real $a_1, a_2, a_3, … , a_n$ fungsi polinomial $x$ dengan pangkat $n$ didefinisikan: $$ f(x)=a_nx^n + a_{n-1}x^{n-1}+ a_{n-2}x^{n-2} + … + a_1x + a_0 $$

Keterangan :

  • $ n =$ derajat suku banyak dengan $ n$ adalah bilangan cacah ,
  • $ a_n, a_{n-1},…,a_1$ adalah *koefisien* suku banyak dengan $a_n \neq 0 $ ,
  • $ a_nx^n$ adalah suku pertama,
  • $ a_{n-1}x^{n-1}$ adalah suku kedua, dan seterusnya.
  • $ a_0 $ adalah suku tetap

Contoh Fungsi Polinomial

  • $f(x)=4$
  • $f(x)=3x-1$
  • $f(x)=x^2-3x-5$
  • $f(x)=6x^3-3x^2-7$

dari keempat contoh diatas yang merupakan fungsi kuadrat adalah point ketiga, karena variabel pangkat tertingginya dua.

Bentuk Umum Fungsi Kuadrat

Fungsi kuadrat adalah fungsi polinomial dengan derajat tertingginya dua.

Bentuk umum dari fungsi kuadrat adalah sebagai berikut: $$f(x)=ax^2+bx+c$$ dengan $a,b,c\in$ bilangan real dan $a \not = 0$

keterangan:

  • $f(x)$ adalah fungsi kuadrat.
  • $a$ dan $b$ adalah koefisien.
  • $c$ adalah konstanta.
  • $x$ yakni sebagai variable. variabel ini sebenarnya tidak harus $x$ ya, bisa huruf apa saja. Namun kalau untuk grafik fungsi ya lebih baik $x$

Jika digambarkan dalam bidang kartesius, grafik fungsi kuadrat berbentuk parabola yang simetris. Bentuk umum dari persamaan grafik fungsi kuadrat dinyatakan $$y=ax^2+bx+c$$

Contoh Soal Fungsi Kuadrat

  1. Manakah dari fungsi berikut yang merupakan fungsi kuadrat?

    1. $f(x)=x²-1$
    2. $f(x)=3x-2²$
    3. $f(x)=4\sqrt{x+4}$
    4. $f(x)=\frac14(2+x)(x²-1) $
    5. $f(x)=(1+x)(1-x)$
    6. $f(x)=x²-8x+15$

    Alternatif Penyelesaian ✍️

    ingat! fungsi kuadrat mempunyai ciri-ciri pangkat tertinggi variabelnya adalah 2 (derajat tertingginya dua), dan hanya mempunyai 1 variabel. mari kita analisa satu-satu

    1. $f(x)=x²-1$ merupakan fungsi kuadrat karena memenuhi kriteria
    2. $f(x)=3x-2²$ bukan merupakan fungsi kuadrat karena derajat variabel x nya 1 (merupakan fungsi linear)
    3. $f(x)=4\sqrt{x+4}$ bukan merupakan fungsi kuadrat (karena derajat tertinggi variabelnya 1 dan diakar)
    4. $f(x)=\frac14(2+x)(x²-1) $ bukan merupakan fungsi kuadrat jika dijabarkan membentuk fungsi kubik (derajat tertingginya 3)
    5. $f(x)=(1+x)(1-x)$ merupakan fungsi kuadrat, jika dijabarkan menghasilkan $f(x)=1-x^2$
    6. $f(x)=x²-8x+15$ merupakan fungsi kuadrat karena memenuhi kriteria

    Jadi, yang merupakan fungsi kuadrat adalah a, e, f. 😄

  2. Diketahui fungsi $f(x) = x² - 3x - 40$. Hitunglah bayangan dari $f(x)$ untuk nilai $x = 3$!

    Alternatif Penyelesaian ✍️

    semua $x$ diganti dengan 3 $$\begin{align*}f(x)&=x^2-3x-40\\f(3)&=3^2-3(3)-40\\&=9-9-40\\&=-40\end{align*}$$

    Jadi, bayangan dari $f(x)$ untuk nilai $x = 3$ adalah $-40$. 😄

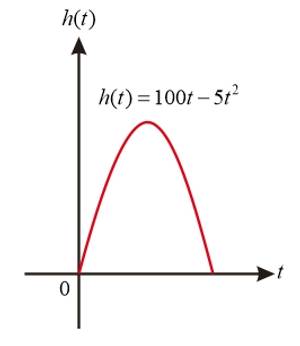
  3. Sebuah roket ditembakkan dari suatu tempat dengan arah dan kecepatan awal tertentu. Ternyata, lintasan roket tersebut membentuk fungsi kuadrat $h(t)=100t-5t^2$ dengan $h(t)$ adalah tinggi roket (dalam m) setelah $t$ detik.

    1. Berapa ketinggian roket setelah 4 detik ditembakkan?
    2. kapan roket berada pada ketinggian 500 m?

    Alternatif Penyelesaian ✍️

    Jika digambarkan, lintasan roket akan membentuk lengkung seperti berikut Grafik Roket Fungsi Kuadrat

    1. lintasan roket membentuk fungsi kuadrat $h(t)=100t-5t^2$ dengan $h(t)$ adalah tinggi roket (dalam m) setelah $t$ detik, maka ketinggian roket setelah 4 detik ditembakkan dapat diwakili oleh fungsi $h(4)$ atau nilai t diganti dengan 4 (substitusi $t=4$) $$\begin{align*} h(t)&=100t-5t^2 \\ h(4)&=100(4)-5(4)^2 \\ &=400-5(16)\\ &=400-80=320 \end{align*}$$ Jadi, ketinggian roket setelah 4 detik ditembakkan adalah 320 m. 😄
    2. mencari $t$ dengan $h(t)=500$ $$\begin{align*} h(t)&=100t-5t^2 \\ 500&=100t-5t^2 \\ 5t^2-100t+500&=0\\t^2-20t+100&=0\\ (t-10)(t+10)&=0\\ t=10 \end{align*}$$ Jadi, roket berada pada ketinggian 500 m saat 10 detik setelah ditembakkan. 😄

Latihan Soal Fungsi Kuadrat

Untuk mendalami materi ini agar kamu lancar, silakan kerjakan soal dibawah ini ya

  1. Manakah dari fungsi berikut yang merupakan fungsi kuadrat?

    1. $f(x)=3x²-4$
    2. $f(x)=3^2x-x²+4$
    3. $f(x)=\sqrt{x^2-6+9}$
    4. $f(x)=\dfrac{(2+x)(x²-1)}{x} $
    5. $f(x)=(x-3)(1-x)$
    6. $f(x)=8x+2y^2+15$

  2. Diketahui fungsi $f(x) = 2x² - 3x - 12$. Hitunglah bayangan dari $f(x)$ untuk nilai $x = -2$!

  3. Diketahui fungsi $f(x) = x² - 5x - 24$. Carilah nilai $x$ jika $f(x)=-10$!

  4. Kadar suatu jenis obat (dalam mg) setelah diminum dinyatakan dalam fungsi $K(t)=8t-t^2$ dengan $t$ adalah waktu (dalam jam) dan $K(t)$ adalah kadar obat.

    1. Berapa kadar obat setelah 3 jam diminum?
    2. Jika Pak Kuat minum obat pukul 07.00, kapan kadar obat tersebut benar-benar habis?

Demikian materi terkait pengertian dan bentuk umum fungsi kuadrat beserta contohnya. Selanjutnya kamu akan mempelajari grafik fungsi kuadrat, yang penting kamu pahami materi ini ya agar di materi selanjutnya bisa lancar..