Ingin menguasai materi lingkaran dan busur lingkaran? Artikel ini akan membantumu! Pelajari definisi, unsur-unsur, dan hubungan sudut pusat serta sudut keliling dengan contoh soal yang mudah dipahami.
Daftar Isi
Hai Sobat Belajar! Pernahkah kamu memperhatikan roda sepeda atau jam dinding? Kedua benda itu memiliki bentuk dasar yang sama, yaitu lingkaran. Lingkaran adalah salah satu bangun datar yang paling sederhana namun memiliki peran penting dalam kehidupan kita. Dalam artikel ini, kita akan mempelajari lebih dalam tentang lingkaran, mulai dari pengertian, unsur-unsur, busur lingkaran, sudut pusat dan sudut keliling. Materi ini merupakan bagian dari materi mata pelajaran Matematika Fase F kelas XI kurikulum merdeka. Adapun capaian pembelajaran materi ini yaitu Peserta didik dapat menerapkan teorema tentang lingkaran, dan menentukan panjang busur dan luas juring lingkaran untuk menyelesaikan masalah (termasuk menentukan lokasi posisi pada permukaan Bumi dan jarak antara dua tempat di Bumi)
1. Pengertian Lingkaran
Lingkaran adalah bangun datar sederhana (geometri datar) yang terbentuk dari semua titik yang berjarak sama terhadap suatu titik tetap yang disebut titik pusat. Jarak dari titik pusat ke setiap titik pada lingkaran disebut jari-jari (r), sedangkan garis lurus yang melalui titik pusat dan menghubungkan dua titik pada lingkaran disebut diameter (d). Hubungan antara jari-jari dan diameter adalah d = 2r.
Lingkaran dan Daerah Lingkaran
Titik tertentu tersebut disebut pusat lingkaran. Jarak tertentu disebut jari- jari lingkaran tersebut. Jarak tersebut biasa dilambangkan r. Pada konteks tertentu, jari-jari dimaksudkan sebagai ruas garis sepanjang pusat ke titik pada lingkarannya.
 Daerah yang dibatasi oleh sebuah lingkaran disebut daerah lingkaran.
Daerah yang dibatasi oleh sebuah lingkaran disebut daerah lingkaran.
Perhatikan gambar lingkaran berikut
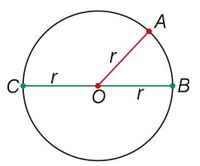 Pada gambar diatas titik O merupakan titik pusat lingkaran. Jarak titik O ke titik A dan jarak titik O ke B sama. Oleh karena itu, ruas garis OA dan ruas garis OB dinamakan jari-jari lingkaran O. sedangkan ruas garis CB melewati titik pusat lingkaran O disebut dengan diameter.
Pada gambar diatas titik O merupakan titik pusat lingkaran. Jarak titik O ke titik A dan jarak titik O ke B sama. Oleh karena itu, ruas garis OA dan ruas garis OB dinamakan jari-jari lingkaran O. sedangkan ruas garis CB melewati titik pusat lingkaran O disebut dengan diameter.
2. Unsur-Unsur Lingkaran
- Pusat lingkaran: Titik tengah lingkaran.
- Jari-jari: Garis lurus yang menghubungkan pusat lingkaran dengan titik pada lingkaran.
- Diameter: Garis lurus yang melalui pusat lingkaran dan menghubungkan dua titik pada lingkaran.
- Tali busur: Garis lurus yang menghubungkan dua titik pada lingkaran, tetapi tidak melalui pusat.
- Busur: Bagian dari lingkaran yang dibatasi oleh dua titik.
Perhatikan gambar berikut
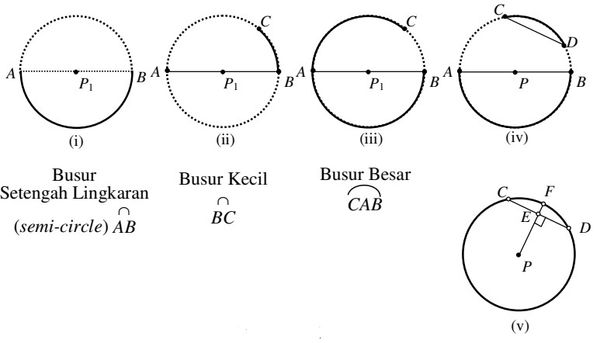
Bagian dari sebuah lingkaran dinamakan busur lingkaran. Ada busur setengah lingkaran, busur kecil (minor) dan busur besar (mayor). Jika tidak dinyatakan lain, maka umumnya yang dimaksud adalah busur kecil. Untuk menegaskan, busur besar ditandai tiga titik. Pada gambar diatas garis lengkung BC merupakan busur lingkaran dan disimbolkan dengan
Ruas garis penghubung dua titik ujung busur pada lingkaran dinamakan tali busur. Pada gambar diatas adalah talibusur. Demikian juga . Talibusur terpanjang, yaitu yang melalui pusat lingkaran, misalnya dinamakan garis tengah (diameter). Panjang diameter, , adalah . Kedua titik ujungnya dinamakan pasangan titik diametral. Dalam konteks tertentu diameter dimaksudkan selain sebagai ruas garis hubung ujung sebuah setengah lingkaran juga ukuran panjang ruas garis tersebut.
Pada Gambar (v), di . Ruas garis dinamakan apotema pada talibusur , dan dinamakan anak panah.
3. Sudut Pusat dan Sudut Keliling
Pada lingkaran, terdapat dua jenis sudut yang penting, yaitu:
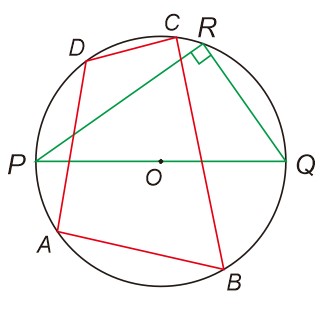
- Sudut pusat: Sudut yang titik sudutnya terletak di pusat lingkaran.
- Sudut keliling: Sudut yang titik sudutnya terletak pada lingkaran.
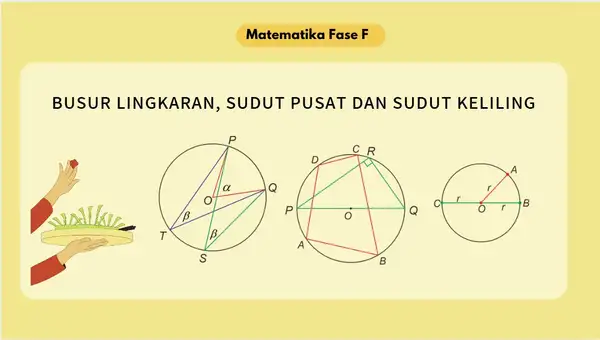
Perhatikan gambar berikut
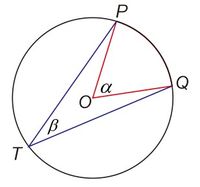 Pada gambar diatas Sudut atau adalah sudut pusat yang menghadap busur . sedangkan sudut atau adalah sudut keliling yang menghadap busur
Pada gambar diatas Sudut atau adalah sudut pusat yang menghadap busur . sedangkan sudut atau adalah sudut keliling yang menghadap busur
Ukuran besar busur dinyatakan dengan busur .
4. Hubungan Sudut Pusat dan Sudut Keliling
Hubungan antara sudut pusat dan sudut keliling sangat menarik. berikut beberapa hubungan tersebut
Dalam sebuah lingkaran, besar sudut pusat = 2 x besar sudut keliling yang menghadap busur yang sama dalam lingkaran tersebut.

Dalam sebuah lingkaran, semua sudut keliling yang menghadap busur yang sama, sama besar. Pada gambar diatas
Sudut keliling yang menghadap busur setengah lingkaran besarnya 90°.()

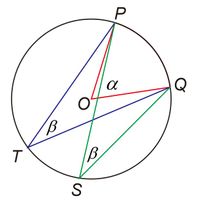
Jika keempat titik sudut segi empat ABCD terletak pada sebuah lingkaran, maka jumlah besar sudut yang berhadapan adalah 180°.
dan
Contoh Soal
Diketahui pada lingkaran O terdapat titik K, L, dan M. Jika , tentukan !
Alternatif Penyelesaian ✍️
Titik O merupakan pusat lingkaran sehingga merupakan sudut pusat dan sudut keliling.Diketahui pada gambar berikut adalah . Tentukan !.

Alternatif Penyelesaian ✍️
Amati gambar berikut!.
 Hitunglah nilai dari gambar di atas!
Hitunglah nilai dari gambar di atas!Alternatif Penyelesaian ✍️
cari sudut
cari nilai x
Demikian artikel tentang Lingkaran dan Busur Lingkaran. Dengan memahami definisi, unsur-unsur, dan hubungan antara sudut pusat dan sudut keliling, kamu akan lebih mudah menyelesaikan soal-soal yang berkaitan dengan lingkaran. Selamat belajar!
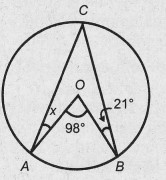 Hitunglah nilai
Hitunglah nilai