Berikut ini adalah contoh soal barisan deret aritmetika kelas 10 fase e elemen bilangan yang bisa kamu pelajari lengkap dengan pembahasan.

Barisan dan deret merupakan salah satu materi dalam pelajaran matematika yang merupakan bagian dari elemen bilangan. Materi ini tentunya kamu pelajari di kelas X Fase E ya. Kali ini kita fokus ke barisan dan deret aritmetika dulu ya

Untuk teorinya bisa kamu pelajari tentang Barisan Dan Deret Aritmetika, Rumus Dan Penerapannya↝ .

Oke langsung saja berikut adalah contoh soal barisan dan deret aritmetika beserta pembahasannya

Soal Pola Barisan

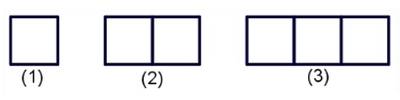
  1. Perhatikan pola yang dibentuk dari potongan lidi berikut ini! Potongan Lidi Pola Barisan Banyak potongan lidi pada pola ke-55 adalah…

    1. 166
    2. 169
    3. 170
    4. 175
    5. 180

    Alternatif Penyelesaian ✍️

    pola potongan lidi 4, 7, 10, …

    di dapat pola $U_n=3n+1$, Sehingga $$U_{55}=3(55)+1=165+1=166$$

    Ans: A πŸ˜„

  2. Gambar berikut adalah segitiga yang disusun dari batang korek api. Potongan Lidi Pola Barisan Banyak batang korek api yang diperlukan untuk membuat pola ke-7 adalah…

    1. 45
    2. 63
    3. 84
    4. 108
    5. 116

    Alternatif Penyelesaian ✍️

    Dari Gambar terlihat

    pola 1 : $1\times3$
    pola 2 : $(1+2)\times3$
    pola 3 : $(1+2+3)\times3$

    di dapat pola $U_7=(1+2+3+…+7)\times 3$, Sehingga $$U_{7}=\frac12\times 7(7+1)\times 3\\U_{7}=\frac12\times 7\times 8\times 3\\U_{7}= 7\times 4\times 3 =84 $$

    Ans: C πŸ˜„

  3. Tiga suku berikutnya dari barisan 25, 27, 30, 34, β‹― adalah…

    1. 39, 42, 46
    2. 38, 43, 49
    3. 39, 44, 49
    4. 39, 45, 52
    5. 38, 45, 49

    Alternatif Penyelesaian ✍️

    $\underbrace{25, 27}_{+2} \underbrace{, 30 }_{+3} \underbrace{, 34 }_{+4} \underbrace{, … }_{+5} \underbrace{, … }_{+6} \underbrace{, … }_{+7}$

    Jadi, jawabannya adalah 39, 45, 52

    Ans: D πŸ˜„

  4. Diberikan barisan 81, 2, 27, 6, 9, 18, a, Nilai b dan a adalah…

    1. 54 dan 3
    2. 3 dan 54
    3. 3 dan 45
    4. 45 dan 3
    5. 4 dan 35

    Alternatif Penyelesaian ✍️

    Ans: A

  5. Jika rumus suku ke-n dari suatu barisan adalah $U_n = 5 – 2n^2$, maka selisih suku ketiga dan kelima adalah ….

    1. 32
    2. –32
    3. 28
    4. –28
    5. 25

    Alternatif Penyelesaian ✍️

    Diketahui : $π‘ˆ_𝑛 = 5 βˆ’ 2𝑛^2$

    Ditanyakan : $π‘ˆ_3 βˆ’ π‘ˆ_5 = β‹― ?$

    $$\begin{align*} π‘ˆ_3 βˆ’ π‘ˆ_5&=(5 βˆ’ 2(3)^2)-(5 βˆ’ 2(5)^2)\\ &=(5 βˆ’ 2(9))-(5 βˆ’ 2(25))\\ &=(5 βˆ’ 18)-(5 βˆ’ 50)\\ &=(-13)-(-45)=28\\ \end{align*}$$

    ANS: C πŸ˜„

  6. Rumus suku ke-n dari suatu barisan adalah $U_n = 4 + 2n – an^2$ , Jika suku ke 4 adalah –36 maka nilai a adalah …

    1. –3
    2. –2
    3. 2
    4. 3
    5. 4

  7. Suatu barisan 1, 4, 7, 10, … memenuhi pola $Un = an + b$. Suku ke 10 dari barisan itu adalah

    1. 22
    2. 28
    3. 30
    4. 31
    5. 33

  8. Suatu barisan 2, 5, 10, 17, …. memenuhi pola $Un = an^2 + bn + c$. Suku ke 9 dari barisan itu adalah

    1. 73
    2. 78
    3. 80
    4. 82
    5. 94

  9. Suku pertama suatu barisan adalah 4, sedangkan suku umum ke-n (untuk n > 1) ditentukan dengan rumus Un = 3.Un–1 – 5. Suku ke tiga adalah …

    1. 16
    2. 14
    3. 13
    4. 12
    5. 10

  10. Pola bilangan untuk barisan 44, 41, 38, 35, 32, … memenuhi rumus …

    1. Un = 44 – n
    2. Un = 46 – 2n
    3. Un = 48 – 4n
    4. Un = 3n + 41
    5. Un = 47 – 3n

Latihan Soal Barisan Aritmetika

  1. Diketahui barisan aritmatika 1,3,5,7,…

    suku ke 10 barisan tersebut adalah…

    1. 15
    2. 16
    3. 17
    4. 18
    5. 19

    Ans: E

  2. Dari barisan 3, 5, 7, 9, 11, … suku ke 21 adalah

    1. 40
    2. 43
    3. 46
    4. 49
    5. 5

  3. Suatu barisan aritmatika diketahui suku ke 4 adalah 6 dan bedanya 3. Suku ke 8 adalah …

    1. 18
    2. 31
    3. 34
    4. 37
    5. 40

  4. Suatu barisan aritmatika diketahui suku ke 15 adalah 30 dan bedanya –5. Suku ke 6 adalah

    1. 65
    2. 25
    3. 75
    4. 80
    5. 90

  5. Rumus umum suku ke-n dari barisan 4, 9, 14, 19, 24, …. adalah …

    1. 5n + 2
    2. 5n – 1
    3. 5n + 1
    4. 5n – 2
    5. 5n + 2

  6. Suatu barisan aritmatika diketahui suku ke 6 adalah –4 dan suku ke 9 adalah –19, maka suku ke 11 adalah…

    1. –34
    2. –29
    3. –19
    4. –24
    5. –14

Latihan Soal Deret Aritmetika

  1. Hasil dari 5 + 7 + 9 + 11 + … + 41 adalah …

    1. 379
    2. 437
    3. 471
    4. 407
    5. 207

  2. Jika 4 + 6 + 8 + 10 + … + x = 130, maka nilai x adalah …

    1. 10
    2. 15
    3. 18
    4. 22
    5. 32

  3. Suku ke empat dari suatu barisan aritmatika adalah 20 dan jumlah 5 suku pertamanya sama dengan 80. Jumlah sebelas suku pertamanya adalah…

    1. 196
    2. 210
    3. 264
    4. 308
    5. 332

  4. Dari suatu deret aritmatika diketahui jumlah n suku pertamanya ditentukan dengan rumus $S_n =𝑛^2(3n + 5)$. Suku ke 6 adalah …

    1. 19
    2. 33
    3. 36
    4. 39
    5. 42

  5. Jumlah bilangan bulat antara 10 dan 60 yang habis dibagi 3 adalah

    1. 552
    2. 486
    3. 462
    4. 312
    5. 396

  6. Seorang ayah menabung uangnya di rumah. Setiap bulan besar tabungan bertambah secara tetap dimulai dari bulan pertama Rp50.000,00, bulan kedua Rp55.000,00, bulan ketiga Rp60.000,00, dan seterusnyJumlah tabungan selama 10 bulan adalah …

    1. Rp500.000,00,
    2. Rp550.000,00,
    3. Rp600.000,00,
    4. Rp700.000,00,
    5. Rp725.000,00,

    Ans: E

  7. Seorang petani sayuran mencatat hasil panennya selama 10 hari berturut-turut. Hasil panen hari pertama 24 kg dan setiap hari berikutnya bertambah 3 kg dari hasil panen hari sebelumnyJumlah hasil panen selama 10 hari tersebut adalah …

    1. 220 kg
    2. 255 kg
    3. 375 kg
    4. 390 kg
    5. 750 kg

    Ans: C