Belajar Konsep Jarak Pada Dimensi Tiga mulai Materi Matematika Kelas XI Fase F. Simak rumus dan contoh soal konsep jarak titik ke titik berikut
Daftar Isi
Sobat Sinmat, Kali ini kita akan belajar tentang materi dimensi tiga pada mata pelajaran matematika untuk kelas XI atau Fase F atau kelas XII di kurikulum 2013 ya. Dimensi Tiga banyak ditemukan di kehidupan sehari-hari, lho! Misalnya, yaitu kamar rumah kamu bisa berbentuk kubus, akuairum ikan, kolam renang berbentuk balok.
Semua bangun ruang tersebut terdiri dari tiga komponen dasar, yakni titik, sudut, dan juga bidang. Dari komponen tersebut dapat diperoleh sudut dan juga jarak yang ada. Kali ini di kelas XI kita akan fokus pada menentukan jarak antar titik, jarak antar titik ke garis, dan jarak antar titik ke bidang!
Sebelum lanjut ke jarak pada bangun ruang ini, kamu perlu paham dulu materi prasayatnya yaitu teorema pythagoras. Masih ingatkan?
Teorema Pythagoras
Agar lebih jelas, Perhatikan gambar berikut
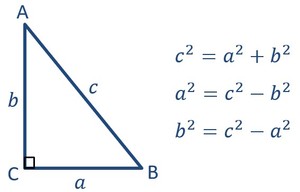
Oke, selanjutnya kita masuk ke jarak pada dimensi tiga ya
1. Konsep Jarak Secara Umum dalam Dimensi Tiga
Misalkan diketahui balok ABCD.EFGH kita dapat menentukan jarak titik A ke garis BH dengan cara mmemroyeksikan titik A ke garis BH. Kita dapat menentukan jarak tersebut dengan membuat segitiga bantu ya..
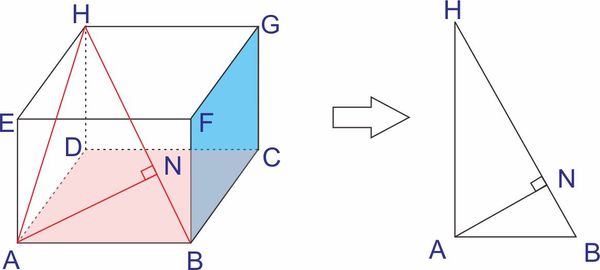
2. Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Contoh Soal 1 Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak antara titik-titik berikut.
- B ke F
- A ke D
- G ke H
- A ke C
- H ke B
- G ke titik tengah AB
Penyelesaian
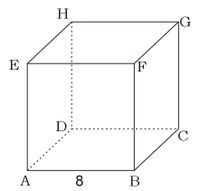
- Jarak titik B ke F diwakili oleh panjang ruas garis (rusuk) BF. Jadi, jarak titik B ke F adalah 8 cm.
- Jarak titik A ke D diwakili oleh panjang ruas garis (rusuk) AD. Jadi, jarak titik A ke D adalah 8 cm.
- Jarak titik G ke H diwakili oleh panjang ruas garis (rusuk) GH. Jadi, jarak titik G ke H adalah 8 cm.
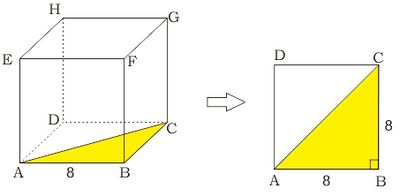
- Jarak titik A ke C diwakili oleh panjang ruas garis AC. Ruas garis AC merupakan diagonal bidang alas ABCD.
 Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.
Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm. - Jarak titik B ke H diwakili oleh panjang ruas garis BH. Ruas garis BH merupakan diagonal ruang kubus ABCD.EFGH.
 Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.
Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm. - Misal T adalah titik tengah AB maka jarak G ke titik tengah AB diwakili oleh panjang ruas garis TG
 Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Contoh Soal Sehari-hari, Jarak Titik ke Titik pada Bangun Ruang atau Dimensi Tiga
Pak Dimen mempunyai kamar tidur yang berukuran 3m × 3m × 4m. Tepat di tengah plafon kamar dipasang lampu. Jika saklar lampu diletakkan tepat di tengah salah satu dinding kamar, berapakah jarak dari lampu ke saklar?
Penyelesaian
Kita gambar dalam bentuk balok ABCD.EFGH
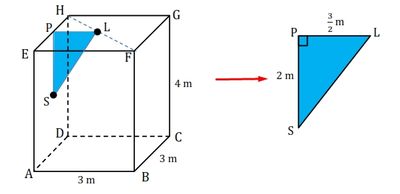 Misalkan lampu (L), saklar (S) berada di dinding ADHE, dan P adalah titik tengah EH. Jarak antara lampu dan saklar adalah LS.
Misalkan lampu (L), saklar (S) berada di dinding ADHE, dan P adalah titik tengah EH. Jarak antara lampu dan saklar adalah LS.
Perhatikan $\vartriangle LPS$ siku-siku di P. Dengan menggunakan teorema pythagoras kita peroleh $$\begin{align*}\tag{teorema pythagoras}LS^2&=PS^2+PL^2\\ &=2^2+\begin{pmatrix} \frac{3}{2} \end{pmatrix}^2\\&=4+\frac{9}{4}\\&=\frac{16}{4}+\frac{9}{4}=\frac{25}{4}\\ LS&=\sqrt{\frac{25}{4}}\\ LS &=\frac{5}{2}=2,5 \end{align*}$$ Jadi, jarak lampu ke saklar adalah $2,5$ cm.
3. Latihan Soal
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Hitunglah jarak antar titik-titik berikut.
- titik A dan G
- titik D dan F
- titik B dan titik tengah garis EG
- titik E dan titik tengah garis BG
Diketahui balok ABCD.EFGH dengan panjang rusuk AB = 8 cm, BC = 6 cm, dan AE = 9 cm. Titik M merupakan titik potong antara diagonal AC dan BD. Rusuk CG diperpanjang 3 cm, kemudian dari titik M ditarik garis miring sehingga memotong perpanjangan rusuk CG di titik N. Hitung panjang ruas garis MN yang terjadi dan buat sketsa permasalahan tersebut.
Demikian artikel mengenai konsep jarak titik ke titik pada bangun ruang. Silahkan dicoba untuk berlatih soal-soal. Banyak sekali soal tentang konsep jarak ini. Tidak semudah teorinya. Ingat banyaklah berlatih biar lebih mahir.
 Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.
Dari gambar di atas, kita perhatikan bahwa segitiga ABC adalah segitiga siku-siku di B. Berdasarkan Teorema Pythagoras diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}AC^2&=AB^2+BC^2\\ \tag{panjang AB=BC=8} &=8^2+8^2\\&=64+64\\&=64\times 2\\ AC&=\sqrt{64\times 2}=\sqrt{64}\times\sqrt{2}\\ AC &=8\sqrt{2} \end{align*}$$
Jadi, jarak titik A ke C adalah $8\sqrt{2}$ cm.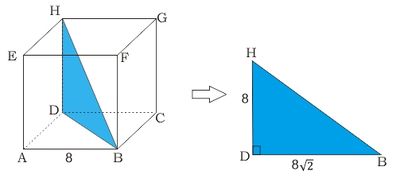 Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.
Dari gambar, kita peroleh $\vartriangle BDH$ adalah segitiga siku-siku di D. BD merupakan diagonal bidang alas dengan panjang sama dengan AC sehingga $BD=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle BDH$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}BH^2&=BD^2+DH^2\\ &=(8\sqrt{2})^2+8^2\\&=128+64\\&=192=64\times 3\\ AC&=\sqrt{64\times 3}=\sqrt{64}\times\sqrt{3}\\ AC &=8\sqrt{3} \end{align*}$$
Jadi, jarak titik B ke H adalah $8\sqrt{3}$ cm.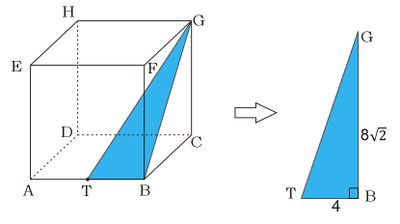 Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.
Dari gambar, kita peroleh $\vartriangle TBG$ siku-siku di B. BG merupakan diagonal bidang dengan panjang sama dengan AC sehingga $BG=AC=8\sqrt{2}$. Berdasarkan Teorema Pythagoras pada $\vartriangle TBG$ diperoleh hubungan:
$$\begin{align*}\tag{teorema pythagoras}TG^2&=TB^2+BG^2\\ &=4^2+(8\sqrt{2})^2\\&=16+128\\&=144\\ AC&=\sqrt{144}\\ AC &=12 \end{align*}$$
Jadi, jarak titik G ke titik tengah AB adalah $12$ cm.