Dimensi Tiga: Kedudukan Titik, Garis, Bidang

Menentukan kedudukan titik, garis, dan bidang dalam ruang. Dimensi Tiga merupakan materi matematika bidang geometri.

1. Pengertian Titik, Garis, Bidang, dan Bangun Ruang

Sering kita mendengar istilah titik, garis, dan bidang baik dalam kehidupan sehari-hari maupun didalam pembelajaran di sekolah terutama mata pelajaran Matematika. Ketiga istilah tersebut merupakan unsur dasar dalam geometri. Ketiga unsur tersebut termasuk istilah yang tidak didefinisikan (undefined term) karena secara intuitif dianggap sebagai sesuatu yang mudah dijelaskan.

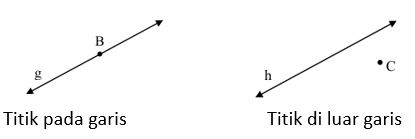
Titik merupakan sesuatu yang punya kedudukan, tetapi titik tidak punya ukuran. Titik direpresentasikan sebagai noktah/dot (“.”) dan dinamai dengan huruf kapital. Pada gambar berikut diperlihatkan dua buah titik, yaitu titik B dan titik Q.

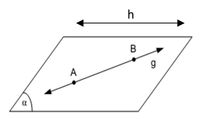
Garis merupakan sesuatu/benda berdimensi satu dan hanya mempunyai panjang tapi tidak mempunyai lebar. Garis diberi nama dengan menggunakan huruf kecil seperti g,h,k, dan seterusnya, atau AB, AC, BC, dan seterusnya. Pada gambar berikut diperlihatkan dua buah garis, yaitu garis h dan ruas garis AC.

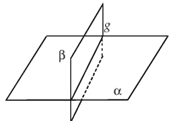
Bidang (bidang datar) merupakan sesuatu/benda berdimensi dua yang mempunyai ukuran panjang dan lebar. Bidang dapat dinamai dengan cara menuliskan di pojok bidang dengan huruf α, β, γ atau dengan menuliskan titik-titik sudut bidang itu.

Bangun ruang adalah benda berdimensi tiga yang mempunyai ukuran panjang, lebar, tebal/tinggi. Contoh dari bangun ruang ini adalah balok, kubus, prisma, dan lain-lain.

2. Kedudukan Titik dan Garis

1. Titik Terletak pada Garis Sebuah titik dikatakan terletak pada garis, jika titik tersebut dapat dilalui oleh garis. Perhatikan gambar 2.5.
2. Titik di Luar Garis Sebuah titik dikatakan terletak di luar garis, jika titik tersebut tidak dapat dilalui garis. Perhatikan gambar 2.6

3. Kedudukan Titik dan Bidang

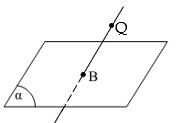
1. Titik Terletak pada Bidang Sebuah titik dikatakan terletak pada bidang, jika titik tersebut dapat dilalui oleh bidang.
2. Titik di Luar Bidang Sebuah titik dikatakan terletak di luar bidang, jika titik tersebut tidak dapat dilalui oleh bidang.

4. Kedudukan Dua Garis

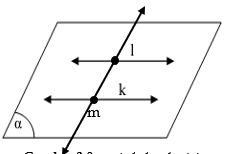
1. Dua Garis Sejajar Dua buah garis dikatakan sejajar, jika dua buah garis tersebut sebidang dan tidak mempunyai titik persekutuan. garis $k$ dan $l$ sejajar, garis $m$ berpotongan dengan $k$ dan $l$
2. Dua Garis Berpotongan Dua buah garis dikatakan berpotongan, jika dua buah garis tersebut sebidang dan mempunyai satu titik persekutuan, yang dinamakan titik potong. Perhatikan gambar diatas.
3. Dua Garis Berimpit Dua garis dikatakan berimpit, jika jarak antara kedua garis tersebut adalah nol. garis $k$ berimpit dengan garis $l$
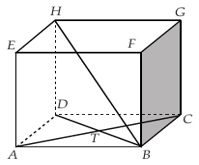
4. Dua Garis Bersilangan Dua buah garis dikatakan bersilangan, jika dua buah garis tersebut tidak sebidang atau melalui kedua garis tersebut tidak dapat dibuat sebuah bidang datar. garis HB dan GC bersilangan

5. Kedudukan Garis dan Bidang

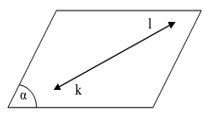
1. Garis Terletak pada Bidang Sebuah garis dikatakan terletak pada bidang, jika setiap titik pada garis tersebut juga terletak pada bidang. garis g pada bidang $\alpha$ dan garis h sejajar bidang $\alpha$
2. Garis Sejajar Bidang Sebuah garis dikatakan sejajar bidang, jika garis dan bidang tidak mempunyai satu pun titik persekutuan.
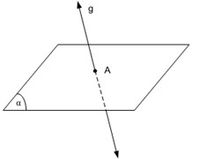
3. Garis Memotong (Menembus) Bidang Sebuah garis dikatakan memotong (menembus) bidang, jika garis dan bidang mempunyai satu titik persekutuan yang dinamakan titik potong atau titik tembus. garis g menembus bidang di titik A

6. Kedudukan Dua Bidang

1. Dua Bidang Berimpit Dua bidang dikatakan berimpit, jika setiap titik terletak pada kedua bidang.
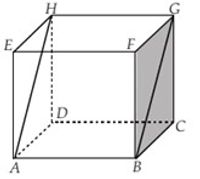
2. Dua Bidang Sejajar Dua bidang dikatakan sejajar, jika kedua bidang tersebut tidak mempunyai satu pun titik persekutuan. Bidang BCGH dan ADHE sejajar
3. Dua Bidang Berpotongan Dua bidang dikatakan berpotongan, jika kedua bidang tersebut mempunyai sebuah garis persekutuan. Bidang $\alpha$ dan $\beta$ berpotongan

Contoh Melukis garis, Bidang

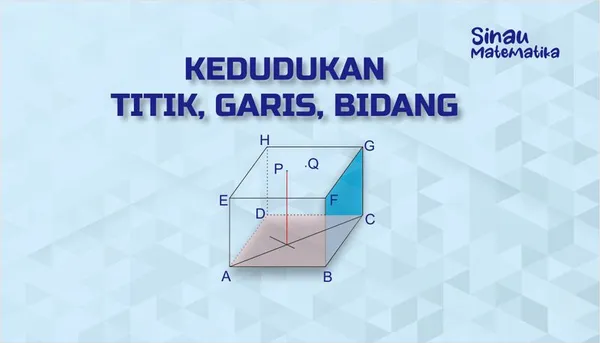
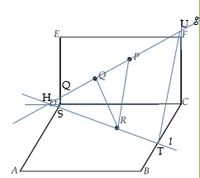
Pada gambar berikut ini, titik Pdan Q pada bidang DCFE, titik R pada bidang ABCD. Lukislah garis potong antara bidang ABCD dan bidang yang melalui titik-titik P,Q, dan R. Lukislah juga garis potong antara bidang DCFE dan bidang yang melalui titik-titik P, Q, dan R!

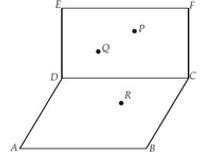
Jawab:

1. Buat garis yang melalui PQ memotong garis CD yang merupakan garis tumpuan bidang DCFE dan bidang ABCD. Perpotongan garis ini adalah titik H.
2. Buatlah garis RH.
3. Terbentuklah bidang PQR. Bidang ini berimpit dengan bidang UQST.
4. Garis g pada gambar merupakan garis potong antara bidang DCFE dan bidang yang melalui titik-titik P, Q, dan R.
5. Garis l pada gambar merupakan garis potong antara bidang ABCD dan bidang yang melalui titik-titik P, Q, dan R.