Fungsi Komposisi Fase F Kelas XI Pengertian Rumus Contoh

Fungsi komposisi yaitu penggabungan beberapa fungsi yang dipelajari pada fase F kelas XI, simak pengertian, rumus, contoh penjelasannya disini!

Salam jumpa Sobat Sinmat. Kali ini kita akan bersama belajar matematika dengan materi Fungsi Komposisi yang dipelajari pada Kelas XI Fase F Kurikulum Merdeka. Apa itu Fungsi Komposisi? Fungsi komposisi merupakan proses penggabungan dua fungsi atau lebih.

Oh ya.. Sebelum lanjut, mungkin ada yang belum tau atau lupa apa itu fungsi? Fungsi adalah relasi himpunan A ke himpunan B, dengan setiap anggota A dipasangkan ke tepat satu anggota B.

Fungsi dalam matematika dapat diilustrasikan seperti gambar berikut.

Untuk lebih detailnya silakan baca materi relasi dan fungsi ya.

Nah, setelah tahu apa itu fungsi, gabungan dari beberapa fungsi ini disebut dengan fungsi komposisi!

sebagai ilustrasi, seseorang akan membuat produk mebel kursi tentu melalui beberapa tahapan kan, tahap pemilihan bahan, tahap pengolahan bahan, tahap finising.

Proses di atas dapat kita gambarkan dalam bentuk fungsi sebagai berikut:

Mari kita bahas lebih mendetai tentang fungsi komposisi!

Pengertian Fungsi Komposisi

Fungsi komposisi adalah fungsi yang melibatkan lebih dari satu fungsi. Ketika ada suatu fungsi, kemudian dilanjutkan dengan fungsi lainnya, maka akan membentuk suatu fungsi baru. Fungsi baru inilah merupakan fungsi hasil komposisi dari kedua fungsi sebelumnya.

Misalnya, ada fungsi $f(x)$ dan $g(x)$. Fungsi $f$ komposisi $g$ disimbolkan $(f\circ g) (x)=f(g(x))$ adalah fungsi yang dipetakan oleh fungsi $g(x)$ (fungsi g dikerjakan dulu) kemudian dilanjutkan oleh fungsi $f(x)$. Operasi fungsi komposisi biasa dilambangkan dengan “$\circ$” dan dibaca komposisi atau bundaran.

Misalnya ada fungsi $f(x)$ dan $g(x)$, maka fungsi komposisi yang dapat terbentuk adalah:

1. Fungsi Komposisi $(f\circ g)(x)$

   $(f\circ g)(x)$ dapat dibaca “fungsi $f$ komposisi $g$” atau “$f$ bundaran $g$”, yang artinya fungsi yang dipetakan oleh fungsi $g(x)$ kemudian dilanjutkan oleh fungsi $f(x)$. Jadi, fungsi $g$ nya dikerjakan terlebih dahulu, kemudian hasilnya dimasukkan ke dalam fungsi $f$. Sehingga, dapat dinotasikan sebagai berikut:

   $$(f\circ g)(x) = f(g(x))$$

2. Fungsi Komposisi $(g\circ f)(x)$

   $(g \circ f)(x)$ dapat dibaca “fungsi $g$ komposisi $f$” atau “$g$ bundaran $f$”, yang artinya fungsi yang dipetakan oleh fungsi $f(x)$ kemudian dilanjutkan oleh fungsi $g(x)$. Jadi, fungsi $f$ nya dikerjakan terlebih dahulu, kemudian hasilnya dimasukkan ke dalam fungsi $g$. dapat dinotasikan sebagai berikut:

   $$(f\circ g)(x) = f(g(x))$$

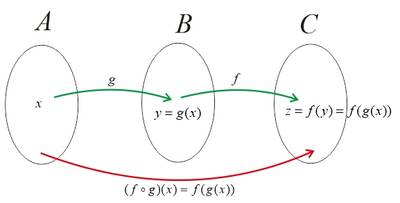
Sebagai ilustrasi, perhatikan gambar berikut: Jika $f : A → B$ ditentukan dengan rumus $f(x)$ dan $g : A → B$ ditentukan dengan rumus $g(x)$, maka hasil dari $f$ komposisi $g$ adalah $h(x) = (f\circ g)(x) = f(g(x))$.

Syarat Fungsi Komposisi

Syarat yang harus dipenuhi agar fungsi $f$ dan fungsi $g$ dapat dikomposisikan menjadi fungsi komposisi $(g \circ f)$ adalah irisan antara daerah hasil fungsi $f$ dan daerah asal fungsi $g$ bukan himpunan kosong, atau $R_f \cap D_g \neq \emptyset$.

Daerah Asal Fungsi Komposisi

• Misalkan terdefinisi fungsi komposisi $(g \circ f)(x)$ , daerah asalnya ($D_{g \circ f}$) adalah

  $D_{g \circ f} = { x | x \in D_f , f(x) \in D_g }$

• Misalkan terdefinisi fungsi komposisi $(f \circ g)(x)$ , daerah asalnya ($D_{f \circ g}$) adalah

  $D_{f \circ g} = { x | x \in D_g , g(x) \in D_f }$

Keterangan :
$D_f =$ daerah asal fungsi $f$
$D_g =$ daerah asal fungsi $g$

Sifat-Sifat Fungsi Komposisi

Fungsi komposisi memiliki sifat-sifat yang bisa kamu lihat pada gambar di bawah ini.

Jika fungsi $f : A → B$, $g : B → C$, $h : C → D$, maka:

1. tidak berlaku sifat komutatif, yaitu $(f \circ g)(x) \neq (g \circ f)(x)$
2. jika $I$ fungsi identitas ($I(x) = x$) berlaku : $(I \circ f)(x) = (f \circ I)(x) = f(x)$;
3. berlaku sifat asosiatif, yaitu : $(f \circ (g \circ h))(x) = ((f \circ g) \circ h)(x)$.

Oke, agar kamu semakin paham dengan fungsi komposisi perhatikan contoh soal di bawah ini ya!

Contoh Soal Fungsi Komposisi

1. Diketahui $f(x) = 3x + 5$ dan $g(x) = 2x – 7$, maka $(f\circ g)(x)$ adalah ….

   Alternatif Penyelesaian ✍️

   $$\begin{align*} (f\circ g)(x) &= f(g(x))\\&= 3g(x) + 5\\&= 3(2x – 7) + 5 \\ &= 6x – 21 + 5 \\ &= 6x – 16\end{align*}$$

   Jadi, $(f\circ g)(x) = 6x – 16$.

2. Diketahui $f(x) = 3x - 2, g(x) = x^2 +2x - 3$.

   1. Tentukan $(g \circ f)(x)$.
   2. Tentukan $(f \circ g)(x)$.
   3. Apakah berlaku sifat komutatif: $g \circ f = f \circ g$?

   Alternatif Penyelesaian ✍️

   1. $(g \circ f)(x)$.

      $$\begin{align*} (g\circ f)(x) &= g(f(x)) \\ &= g(3x - 2) \\ &= (3x - 2)^2 + 2(3x - 2) - 3 \\ &= (9x^2 -12x + 4 ) + (6x-4) - 3 \\ &= 9x^2 -12x + 6x+4-4 - 3 \\ &= 9x^2 - 12x -3 \\ \end{align*}$$

   2. $(g \circ f)(x)$.

      $$\begin{align*}(f \circ g)(x) &= f(g(x)) \\ &= f(x^2 +2x - 3) \\&= 5(x^2 +2x - 3) - 2 \\ & = 5x^2 + 10x - 15 - 2 \\ &= 5x^2 + 10x - 17 \end{align*}$$

   3. Tidak berlaku sifat komutatif karena $(g\circ f)(x) \neq (f \circ g)(x)$ .

Menentukan komponen pembentuk fungsi komposisi

Misal diketahui fungsi $f$ dan fungsi komposisi $(f \circ g)(x)$ , kita diminta menentukan fungsi $g$. Caranya, langsung substitusi bentuk $g(x)$ ke fungsi $f$, maksudnya semua variabel $x$ pada fungsi $f$ digantikan dengan $g(x)$.

Contoh 3. Diketahui fungsi $f(x) = 3x +12$ dan $(f \circ g)(x) = 3x^2 - 12x -24$. Tentukan fungsi $g(x)$!

Alternatif Penyelesaian ✍️

$$\begin{align*} (f \circ g)(x) &= 3x^2 - 12x -24 \\ f(g(x)) &= 3x^2 - 12x -24 \\ 3[g(x)] +12 &= 3x^2 - 12x -24 \\ 3[g(x)] &= 3x^2 - 12x - 24 - 12 \\ 3[g(x)] &= 3x^2 - 12x - 36 \\ g(x) &= \frac{3x^2 - 12x - 36}{3} \\ g(x) &= x^2 - 4x - 12 \end{align*}$$ Jadi, diperoleh fungsi $g(x) = 2x^2 - 3x + 4$

Misal diketahui fungsi $g$ dan fungsi komposisi $(g \circ f)(x)$ , kita diminta menentukan fungsi $f$. Caranya, substitusi bentuk fungsi $g(x)$ ke $f(x)$, ubah $y=g(x)$ menjadi $x=..$ (inversnya), lalu misalkan agar menjadi satu variabel.

Contoh

1. Diketahui fungsi $g(x) = 3x + 2$ dan $(f \circ g)(x) = x - 3$. Tentukan fungsi $f(x)$ nya !

Alternatif Penyelesaian ✍️

$$\begin{align*} (f \circ g)(x) &= x - 3 \\ f(g(x)) &= x - 3 \\ f(3x+2) &= x - 3 \\ \text{misal } p &= 3x+2 \rightarrow x = \frac{p-2}{3} \\ \text{substitusikan } x &= \frac{p-2}{3} \\ f(3x+2) &= x - 3 \\ f(p) &= \left( \frac{p-2}{3} \right) - 3 \\ f(p) &= \frac{p-2}{3} - 3 \\ f(p) &= \frac{p-2}{3} - \frac{9}{3} \\ f(p) &= \frac{p-2-9}{3} \\ f(p) &= \frac{p-11}{3} \end{align*}$$ Sehingga diperoleh : $$f(p) = \frac{p-11}{3} \rightarrow f(x) = \frac{x-11}{3}$$ Jadi, diperoleh fungsi $f(x) = \dfrac{x-11}{3}$

Itu dia penjelasan tentang fungsi komposisi. Semoga kamu bisa lebih paham tentang fungsi komposisi? Jangan lupa untuk terus berlatih soal-soal lainnya, ya!

Latihan Soal Fungsi Komposisi

1. Diketahui $f(x)=x^2+4x-5$ dan $g(x)=2x-1$. Tentukan hasil fungsi komposisi $(g\circ f)(x)$!
2. Jika $f (x) = 3x +1$ dan $(f\circ g) (x) = 6x^2 + 9x +4$, tentukan fungsi $g(x)$!
3. Fungsi $f : R → R$ dan $g : R → R$ ditentukan oleh $f (x) = 2x −1$ dan $g(x) = 5x − x^2$ . Tentukan nilai untuk $(f\circ g)(−1)$!
4. Dari fungsi $f$ dan $g$ diketahui $g(x) = x −1$ dan $(f\circ g)(x) = 4x^2 − x$. Jika $f(a) = 5$, maka tentukan nilai $a$ !