Pelajari konsep garis singgung lingkaran secara mendalam. Artikel ini membahas pengertian, jenis, rumus, dan contoh soal garis singgung. Cocok untuk matematika kelas XI Fase F

Daftar Isi

Hai Sobat Belajar! Kenapa rantai sepeda bisa berputar dengan mulus mengelilingi gear depan dan belakang? Jawabannya terletak pada konsep matematika yang mungkin tidak kita sadari, yaitu garis singgung lingkaran. Dalam artikel ini, kita akan membahas pengertian, jenis, rumus, dan contoh soal garis singgung lingkaran, cocok buat kamu yang sedang mempelajari materi matematika kelas XI Fase F Kurikulum Merdeka.

Apa itu Garis Singgung Lingkaran?

Pengertian Garis Singgung Lingkaran

Garis singgung lingkaran adalah garis lurus yang hanya memotong lingkaran tepat pada satu titik. Titik potong antara garis singgung dan lingkaran disebut titik singgung. Garis singgung memiliki sifat khusus, yaitu selalu tegak lurus dengan jari-jari lingkaran yang ditarik ke titik singgung.

Perhatikan gambar berikut! Pengertian Garis Singgung Lingkaran Gambar di atas menunjukkan lingkaran yang berpusat di titik O dengan diameter PQ. Garis k tegak lurus PQ dan memotong lingkaran di dua titik. Jika k digeser terus menerus ke atas hingga menyentuh titik Q, akan diperoleh garis k’ yang menyinggung lingkaran dan tegak lurus PQ. Garis k disebut garis singgung dan titik Q disebut titik singgung.

Sifat-sifat Garis Singgung Lingkaran

Sifat-sifat garis singgung lingkaran antara lain.

  1. Garis singgung lingkaran hanya melalui satu titik pada lingkaran.
  2. Garis singgung lingkaran tegak lurus terhadap jari-jari atau diameternya.

Untuk lebih jelasnya amati gambar berikut Sifat Garis Singgung Lingkaran Melalui sebuah titik pada lingkaran hanya dapat dibuat satu garis singgung pada lingkaran tersebut.

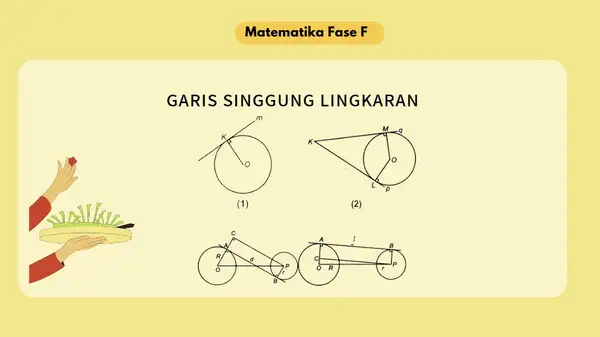
Amatilah gambar (1)!

Diketahui lingkaran O dengan titik K pada keliling lingkaran. Ada garis m yang menyinggung lingkaran O di titik K dan tegak lurus jari-jari OK. Garis m merupakan garis singgung lingkaran.

Melalui sebuah titik di luar lingkaran dapat dibuat dua garis singgung.

Amatilah gambar (2)!

Titik K terletak di luar lingkaran O. Dibuat garis p dan q yang melalui titik K. Garis p menyinggung lingkaran O di titik L, sedangkan garis q menyinggung lingkaran O di titik M. Dalam hal ini, garis p dan q merupakan garis singgung lingkaran.

Rumus Panjang Garis Singgung Lingkaran

Amati gambar berikut! Rumus Garis Singgung Lingkaran Diketahui lingkaran dengan pusat O dan titik A terletak di luar lingkaran O. Dari titik A ditarik garis singgungAB. Garis singgung AB tegak turus jari-jari OB. Berarti, segitiga AOB siku-siku di B. Oleh karena itu, berlaku teorema Pythagoras sebagai berikut: $$AB^2=OA^2-OB^2$$ dengan

  • AB = garis singgung lingkaran,
  • OA = jarak titik A terhadap titik pusat lingkaran,
  • OB = jari-jari lingkaran.

Contoh:

Diketahui dua garis singgung yang ditarik dari titik A di luar lingkaran O. Jika jarak titik A dan O adalah 13 cm dan jari-jari lingkaran O adalah 5 cm, tentukan panjang garis singgung tersebut! Soal Garis Singgung Lingkaran

Alternatif Penyelesaian ✍️

$AB = AC =$ garis singgung; $OA = 13$ cm

$BO= CO =$ jari-jari lingkaran $O = 5$ cm

$$\begin{align*}AB^2&=OA^2-OB^2 \\ &=13^2-5^2\\ &=169-25 \\ AB^2 &= 144 \\ AB&= 12 \end{align*}$$

Jadi, panjang garis singgung AB adalah 12 cm.

Jenis-jenis Garis Singgung Dua Lingkaran

Terdapat beberapa jenis garis singgung lingkaran, antara lain:

  • Garis singgung persekutuan luar: Garis singgung yang terletak di luar dua lingkaran yang berbeda dan menyinggung kedua lingkaran tersebut.
  • Garis singgung persekutuan dalam: Garis singgung yang terletak di antara dua lingkaran yang berbeda dan menyinggung kedua lingkaran tersebut.

Rumus-rumus Garis Singgung Dua Lingkaran

1. Garis Singgung Persekutuan Dalam Dua Lingkaran

Amati gambar berikut! Garis Singgung Persekutuan Dalam Dua Lingkaran Pada gambar diatas, d merupakan garis singgung persekutuan dalam. Panjang d dapat ditentukan dengan rumus berikut. $$d^2=j^2-(R+r)^2$$ dengan

  • d = panjang garis singgung persekutuan dalam;
  • j = jarak kedua pusat lingkaran;
  • R = panjang jari-jari lingkaran pertama (lingkaran besar); dan
  • r = panjang jari-jari lingkaran kedua (lingkaran kecil).

Contoh:

Dua lingkaran masing-masing berpusat di K dan L dengan panjang KL = 11 cm, panjang jari-jari lingkaran A adalah 5 cm, dan panjang jari-jari lingkaran B adalah 4 cm. Hitunglah panjang garis singgung persekutuan dalam dua lingkaran tersebut!

Alternatif Penyelesaian ✍️

Diketahui

  • j = 11 cm
  • R = 5 cm
  • r = 4 cm

Ditanya

  • d= …?

Jawab $$\begin{align*}d^2&=j^2-(R+r)^2 \\ &= 11^2-(5+4)^2 \\&=11^2-9^2 \\ &= 121 -81 \\ d^2 &= 40 \\ d &= \sqrt{40} = 2\sqrt{10}\end{align*}$$

Jadi, panjang garis singgung persekutuan dalam dua lingkaran tersebut adalah $2\sqrt10$ cm.

2. Garis Singgung Persekutuan Luar Dua Lingkaran

Amati gambar berikut! Garis Singgung Persekutuan Luar Dua Lingkaran pada gambar diatas, $l$ merupakan garis singgung persekutuan luar. Panjang d dapat ditentukan dengan rumus berikut: $$l^2=j^2-(R-r)^2$$ dengan

  • $l$ = panjang garis singgung persekutuan luar;
  • j = jarak kedua pusat lingkaran;
  • R = panjang jari-jari lingkaran pertama; dan
  • r = panjang jari-jari lingkaran kedua.

Contoh: Diketahui lingkaran Q dengan panjang jari-jari 14 cm dan lingkaran R dengan panjang jari-jari 30 cm. Jika jarak QR = 34 cm, tentukan panjang garis singgung persekutuan luar dua lingkaran tersebut!

Alternatif Penyelesaian ✍️

  • Diketahui: j = 34 cm; R = 30 cm; r = 14 cm
  • Ditanya: $l = …?$

Jawab $$\begin{align*}l^2&=j^2-(R-r)^2 \\ &= 34^2 - (30-14)^2 \\ &= 34^2 - 16^2 \\ &= 1156 - 256 \\ l^2 &= 900 \\ l&= \sqrt{900} =30\end{align*}$$ Jadi, panjang, garis singgung persekutuan luar dua lingkaran tersebut adalah 30 cm.

Garis singgung lingkaran merupakan konsep penting dalam geometri yang memiliki banyak penerapan dalam kehidupan sehari-hari. Memahami pengertian, jenis, dan rumus-rumus terkait garis singgung akan sangat membantu kamu dalam menyelesaikan berbagai masalah yang berkaitan dengan lingkaran.

Tips Belajar

  • Visualisasi: Gunakan gambar atau diagram untuk memvisualisasikan konsep garis singgung lingkaran.
  • Latihan soal: Kerjakan banyak soal latihan untuk mengasah pemahaman dan kemampuan pemecahan masalah.
  • Diskusi: Diskusikan dengan teman atau guru jika ada materi yang belum dipahami.

Sebagai latihan kerjakan soal berikut

Latihan Soal

  1. Perhatikan gambar berikut! Latihan Soal Garis Singgung Lingkaran Jika diketahui panjang AB = 30 cm dan jari-jari ling- karan A = 18 cm, hitunglah:

    1. panjang garis singgung BC,
    2. luas segitiga ABC, serta
    3. luas layang-layang ACBDl

  2. Diketahui jarak kedua pusat lingkaran adalah 15 cm. Jika jari-jari kedua lingkaran itu masing-masing 5 cm dan 4 cm, hitunglah panjang garis singgung persekutuan dalam dua lingkaran tersebut!

  3. Titik A berada di luar lingkaran yang berpusat di titik P. Dibuat garis singgung AB dan AC. Jika panjang AB = 20 cm dan jari-jari lingkaran = 15 cm, hitunglah panjang AP dan luas PBAC!

  4. Diketahui panjang garis singgung persekutuan luar dari dua buah lingkaran adalah 48 cm, sedangkan jarak kedua titik pusat lingkaran adalah 50 cm. Jika panjang jari-jari lingkaran yang satu adalah 20 cm, hitunglah panjang jari-jari lingkaran yang lain!