Berikut ini penjelasan lengkap tentang Menggambar Grafik Fungsi Kuadrat beserta contoh soal dan pembahasan, simak selengkapnya disini!

Daftar Isi

Grafik fungsi kuadrat $ f(x) = ax^2+bx+c $ secara umum berbentuk lintasan berbentuk parabola yang simetris.

Untuk menggambar grafik fungsi kuadrat perlu kamu ketahui dulu bahwa grafik fungsi kuadrat berupa parabola dan arah atau hadap dari parabolanya tergantung dari nilai $ a$ nya. Nilai $ a $ dari fungsi kuadrat ini juga akan membantu kamu untuk mengetahui jenis titik puncak dari grafik fungsi kuadratnya. Menggambar grafik fungsi kuadrat ini sangat penting karena biasanya ada kaitannya dengan matri lain pada matematika salah satunya dalam materi kalkulus.

Ada dua bentuk grafik fungsi kuadrat yakni terbuka ke atas dan terbuka ke bawah.

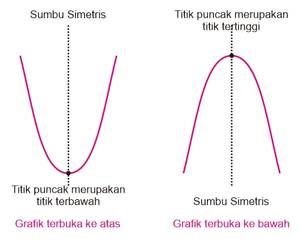
Grafik Fungsi Kuadrat

Pada grafik terlihat bahwa titik puncak berada pada sumbu simetri. Apa itu sumbu simetri? Bagaimana menentukan sumbu simetri?

Sumbu Simetri pada grafik fungsi kuadrat

Garis $ x = x_p $ disebut sumbu simetri yaitu garis yang membagi parabola menjadi dua bagian sama besar ruas kanan dan ruas kiri dari sumbu simetri atau ruas atas dan bawah dari sumu simetri.

Misalkan terdapat fungsi kuadrat $f(x)=ax^{2}+bx+c$

$$\begin{align*} f(x)&=ax^{2}+bx+c\\&=ax^{2}+bx+\frac{b^{2}}{4a}+c-\frac{b^{2}}{4a} \\&=a(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}})+\frac{4ac-b^{2}}{4a} \\&= a(x^{2}+\frac{b}{a}x+(\frac{b}{2a})^{2})+\frac{4ac-b^{2}}{4a} \\&=a(x+\frac{b}{2a})^{2}+\frac{4ac-b^{2}}{4a} \end{align*}$$

Dengan demikian, diperoleh sumbu simetri dari $f(x)$ adalah persamaan garis $x=-\frac{b}{2a}$

Menggambar Sketsa Grafik Fungsi Kuadrat

Sobat Sinmat, bagaimana cara menggambar grafik fungsi kuadrat? sebenarnya mudah dalam menggambar sketsa grafik fungsi kuadrat secara manual, ikuti langkah-langkahnya berikut ya.

Langkah-langkah menggambar sketsa grafik fungsi kuadrat $f(x)=ax^{2}+bx+c$ adalah sebagai berikut.

  1. Tentukan persamaan sumbu simetri $x=-\dfrac{b}{2a}$.

  2. Tentukan koordinat titik puncak. Oleh karena titik puncak $(-\frac{b}{2a},f(-\frac{b}{2a}))$. sumbu simetri, maka koordinat titik puncaknya

  3. Tentukan titik potong dengan sumbu X dan sumbu Y (apabila ada). Jika tidak ada, tentukan titik bantu lain dengan mensubstitusikan sembarang $x\in R$

  4. Gambar sketsa grafik berdasarkan koordinat yang diperoleh.

Contoh Soal dan Pembahasan

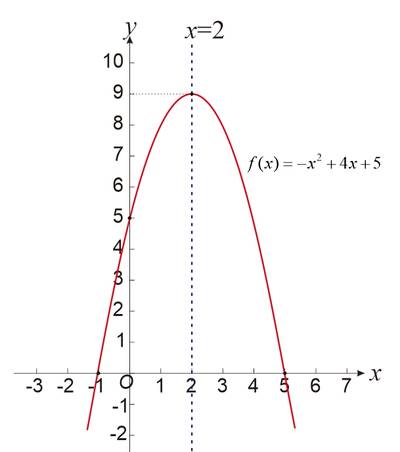
Gambarkan sketsa grafik fungsi kuadrat $f(x)=-x^{2}+4x+5$

Alternatif Penyelesaian ✍️

Diketahui Persamaan fungsi kuadrat $f(x)=-x^{2}+4x+5$ diperoleh nilai $a=-1$, $b=4$, dan $c=5$

  1. Step 1. Menentukan persamaan sumbu simetri.

    Persamaan sumbu simetri:

    Substitusi $a=-1$, $b=4$ ke dalam $x=-\frac{b}{2a}$

    $$\begin{align*}x&=-\frac{b}{2a}\\ x&=-\frac{4}{2(-1)}\\x&=2\end{align*}$$

  2. Step 2. Menentukan Koordinat titik puncak $(-\frac{b}{2a},f(-\frac{b}{2a}))$

    Substitusi $x=2$ ke dalam fungsi kuadrat $f(x)=-x^{2}+4x+5$.

    $$\begin{align*}f(x)&=-x^{2}+4x+5\\ f(2)&=-(2)^{2}+4(2)+5\\ &=-4+8+5\\&=9\end{align*}$$

Jadi, koordinat titik puncaknya (2, 9).

  1. Step 3. Menentukan titik potong terhadap sumbu X dan Y.

    • Grafik akan memotong sumbu X jika $y=0$.

      $y=f(x)=-x^{2}+4x+5$

      $$\begin{gather*}y=-x^{2}+4x+5 \\ 0=-x^{2}+4x+5 \\ x^{2}-4x-5=0\\(x-5)(x+1)=0 \\ x-5=0 \text{ atau } x+1=0 \\ x=5 \text{ atau } x=-1 \end{gather*}$$

      Jadi, titik potong terhadap sumbu X terletak pada koordinat (5, 0) dan (-1, 0).

    • Grafik akan memotong sumbu Y jika $x = 0$.

      $$\begin{align*}f(x)&=-x^{2}+4x+5 \\ f(0)&=-(0)^{2}+4(0)+5 \\ f(0)&=0 \end{align*}$$

      Jadi, titik potong terhadap sumbu Y terletak pada koordinat (0, 5).

  2. Step 4. Gambar sketsa grafik berdasarkan koordinat yang diperoleh.

    Setelah menyelesaikan langkah ssebelumnya diperoleh titik-titik (2,9), (5,0), (-1,0), (0,5) dan sumbu simetrri $x=2$. Diperoleh gambar sketsa grafik fungsi kuadrat $f(x)=-x^{2}+4x+5$ seperti pada gambar di bawah ini.

    contoh soal sketsa grafik fungsi kuadrat

Nilai Maksimum dan minimum fungsi kuadrat

Untuk nilai maksimum dan minimum suatu fungsi kuadrat $ f(x) = ax^2+bx+c $ bisa dilihat dari posisi titik balik yang bergantung dari nilai $ a$ nya.

  • Jika nilai $ a $ positif ($a > 0 $), maka kurva akan menghadap ke atas yang artinya titik baliknya ada di bawah. Pada keadaan ini akan diperoleh nilai minimum.
  • Jika nilai $ a $ negatif ($a < 0 $), maka kurva akan menghadap ke bawah yang artinya titik baliknya ada di atas. Pada keadaan ini akan diperoleh nilai maksimum.

Nilai maksimum atau minimum ini akan berguna pada soal cerita yang berkaitan dengan nilai maksimum dan minimum, materi ini akan diperdalam pada penerapan fungsi kuadrat.

Latihan Soal

Untuk memperjelas pemahamanmu terkait menggambar sketsa grafik fungsi kuadrat, silakan dicoba untuk menggambar sketsa grafik fungsi berikut

  1. $f(x)=x^2-x-12$
  2. $g(x)=2x^2-4x+5$
  3. $h(x)=-x^2-6x-9$

Dari penjelasan dan konsep serta contoh menggambar grafik fungsi kuadrat dengan teknik sketsa langsung, langkah-langkah yang harus kita lakukan yaitu menentukan titik potong grafik pada sumbu-sumbu baik sumbu X maupun sumbu Y, menentukan titik puncak grafik, dan menentukan beberapa titik lain agar grafiknya lebih mulus. SIlakan ikuti

Selanjutnya nanti kita akan mencari fungsi kudrat jika diketahui gambar grafiknya ya..