Pelajari Kaidah Pencacahan! Khususnya Aturan Penjumlahan, Aturan Perkalian, Faktorial, Rumus dan Contoh Soalnya! Baca selengkapnya di sini!
Sobat Sinmat, pernahkah kamu melakukan suatu percobaan? Setiap melakukan suatu percobaan kamu pasti akan selalu mendapatkan hasil. Namun, tidak selalu hasil tersebut sesuai dengan yang diharapkan. Oleh karena itu, dalam melakukan percobaan kita tentu harus menduga hasil yang mungkin terjadi.
Oke, kali ini kita akan belajar tentang Kaidah Pencacahan khususnya tentang Aturan Penjumlahan, Aturan Perkalian dan Notasi Faktorial yang akan kamu gunakan untuk mempelajari Statistika dan Peluang. Sebelum lebih dalam, mari kita pahami dulu tentang kemungkinan suatu kejadian dalam suatu percobaan atau peristiwa.
Perhatikan permasalahan berikut!
Hadi mempunyai tiga buah baju berwarna merah, kuning, dan hitam. Dia juga memiliki dua buah celana berwarna hitam dan kuning. Dapatkah Kamu menentukan pasangan baju dan celana yang dapat dipakai Hadi?
Alternatif Penyelesaian ✍️
Untuk menentukan banyaknya kemungkinan pasangan baju dan celana yang dapat dipakai Hadi dapat menggunakan bantuan tabel atau diagram pohon
- Tabel
 Berdasarkan tabel di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.
Berdasarkan tabel di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning. - Diagram Pohon
 Berdasarkan diagram pohon di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.
Berdasarkan diagram pohon di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.
Itulah salah satu alternatif untuk menyelesaikannya. Ada cara lain secara matematis untuk menentukan banyaknya kejadian/peristiwa secara matematis. Yaitu Aturan perkalian dan Aturan penjumlahan.
Aturan Penjumlahan dalam Kaidah Pencacahan (Rule of Sum)
Jika suatu kejadian yang saling lepas di mana
- kejadian pertama dapat dilakukan dengan cara yang berbeda,
- kejadian kedua dapat dilakukan dengan cara yang berbeda, dan seterusnya. kejadian tersebut dapat dilakukan dengan cara yang berbeda.
Aturan penjumlahan biasanya digunakan untuk beberapa kejadian yang “TIDAK SEKALIGUS TERJADI” artinya yang terjadi hanya salah satu saja dan biasanya menggunakan kata penghubung “ATAU”
Agar kamu tidak bingung dengan istilah diatas, langsung tak kasih contohnya nih..
Sari mempunyai 7 sepatu dan 5 sandal. Pada saat akan bepergian Sari memakai salah satu dari sepatu atau sandal. Ada berapa pilihan yang dapat dipakai Sari?
Alternatif Penyelesaian ✍️
- Banyak sepatu yang dimiliki Sari ada 7. Sari dapat memilih salah satu dari 7 sepatu tersebut.
- Banyak sandal yang dimiliki Sari ada 5. Sari dapat memilih salah satu dari 5 sandal tersebut.
Oleh karena Sari hanya dapat memakai salah satu dari sepatu atau sandal (Masak Sari mau pake Sepatu dan Sandal bareng). Jadi, banyak pilihan yang dimiliki Sari adalah 7+5=12 macam.
Untuk mengikuti kompetisi matematika, sebuah sekolah diwajibkan mengirimkan satu siswa perwakilan. Jika dalam tahap akhir seleksi terpilih 3 siswa laki-laki dan 5 siswa perempuan, tentukan banyaknya cara sekolah tersebut memilih wakilnya untuk mengikuti kompetisi matematika!
Alternatif Penyelesaian ✍️
Pada kasus ini, ada dua pilihan jenis kelamin dari siswa yang akan mengikuti kompetisi yaitu laki-laki dan perempuan. Padahal yang dikirimkan hanya 1 perwakilan, maka harus dipilih salah satu saja. Sehingga kita bisa menggunakan aturan penjumlahan pada kasus ini.- Menentukan banyak cara memilih siswa
Total cara cara. Jadi, ada 8 cara sekolah tersebut memilih wakilnya untuk mengikuti kompetisi matematika.
- Menentukan banyak cara memilih siswa
Dirumah Sandra mempunyai 4 motor dan 10 sepeda, dan 2 mobil. Jika Sandra ingin bepergian sendiri menggunakan kendaraan yang ada dirumah, maka berapa banyak cara Sandra memilih kendaraan tersebut?
Alternatif Penyelesaian ✍️
Tidak mungkin kan Sandra mengendarai ketiganya sekaligus, jadi Sandra hanya memilih 1 kendaraan, pilih motor atau sepeda atau mobil. Maka, dalam kasus ini kita gunakan aturan penjumlahan. Sehingga, banyak cara Sandra memilih kendaraan 4+10+2= 16 cara
Aturan Perkalian dalam Kaidah Pencacahan (Rule of Product)
Aturan ini digunakan ketika dua atau lebih kejadian harus terjadi bersamaan, dan kamu ingin menghitung total banyaknya kejadian. Kamu dapat mengalikan jumlah kejadian masing-masing kejadian.
Jika suatu peristiwa/kejadian dapat terjadi dalam cara yang berbeda dan setelah peristiwa/kejadian itu terjadi, kemudian peristiwa/kejadian itu terjadi dalam cara yang berbeda, dan seterusnya. Peristiwa itu dapat terjadi dalam cara yang berbeda.

Aturan penjumlahan biasanya digunakan untuk beberapa kejadian yang semuanya “EKALIGUS TERJADI” dan biasanya menggunakan kata penghubung “DAN”
Contoh Soal dan Alternatif Penyelesaian
Contoh 1
Rani mempunyai 3 tas dan 2 sepatu. Pada saat akan bepergian Rani memakai salah satu dari tas dan sepatu. Ada berapa pilihan yang dapat dipakai Rani?
Alternatif Penyelesaian ✍️
Banyak tas yang dimiliki Rani ada 3. Rani dapat memilih salah satu dari 3 tas tersebut.
Banyak sepatu yang dimiliki Rani ada 2. Rani dapat memilih salah satu dari 2 sepatu tersebut.
Oleh karena Rani harus memakai keduanya yaitu tas dan sepatu, banyak pilihan yang dimiliki Rani adalah macam.
Contoh 2
Dari huruf-huruf pada kata “LOGIS” akan dibentuk susunan huruf sehingga susunan huruf tidak terdapat huruf yang sama. Berapa banyak cara untuk menyusun huruf-huruf itu jika huruf pertama adalah huruf konsonan?
Alternatif Penyelesaian ✍️
Huruf pertama adalah huruf konsonan, berarti huruf pertama harus huruf L, G, atau S (ada 3 pilihan). Setelah satu huruf digunakan untuk mengisi tempat pertama, selanjutnya tersedia 4 huruf untuk 4 tempat yang lainnya.
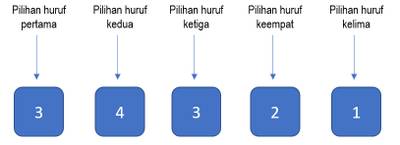 Banyaknya susunan huruf yang mungkin .
Banyaknya susunan huruf yang mungkin .
Contoh 3
Dari angka-angka 1, 3, 4, 5, 7, 8, dan 9 akan dibuat bilangan yang terdiri dari tiga angka berbeda. Berapa banyak bilangan genap yang terbentuk?
Alternatif Penyelesaian ✍️
Disediakan 3 kotak untuk menempatkan angka-angka tersebut. Kotak I tempat ratusan, kotak II tempat puluhan, dan kotak III tempat satuan. Tuliskan dalam masing-masing kotak banyaknya cara menempatkan angka-angka tersebut!
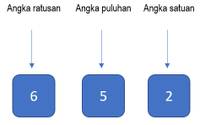 mulai isi kotak dari persyaratan atau angka satuannya yaitu bilangan genap jika angka terakhir genap.
mulai isi kotak dari persyaratan atau angka satuannya yaitu bilangan genap jika angka terakhir genap.
- Pada kotak (satuan) dapat diisi dengan 2 cara, yaitu angka 4 dan 8.
- Pada kotak I (ratusan) dapat diisi dengan 6 cara, karena 1 angka sudah menempati kotak III. Pada kotak II (puluhan) dapat diisi dengan 5 cara, karena 1 angka sudah menempati kotak I dan 1 angka sudah menempati kotak III.
Jadi, banyak bilangan yang dapat disusun adalah .
Contoh 4 Seorang ingin membuatkan plat nomor kendaraan yang terdiri dari 4 angka yang dipilih dari angka-angka 1, 2, 3, 4, 5 dan dalam plat nomor itu boleh ada angka yang sama. Berapa banyak plat nomor dapat dibuat?
Alternatif Penyelesaian ✍️
Soal ini sebenarnya mirip dengan soal nomor (3), hanya saja syaratnya yang dibedakan sedikit.
Plat nomor boleh ada angka yang sama, artinya angka yang sudah dipakai boleh dipakai lagi.
Kita buat 4 kota karena plat nomor terdiri dari 4 angka saja. Pilihan angkarnya adalah 1, 2, 3, 4, 5, artinya totalnya ada 5 pilihan angka. Cara pengisian setiap kotak :
- Kotak I, dapat diisi angka 1, 2, 3, 4, atau 5 sehingga ada 5 cara.
- Kotak II, dapat diisi dengan 5 pilihan angka juga karena angka yang sudah dipakai pada kotak I bisa dipakai lagi pada kotak II.
| 5 | 5 | 5 | 5 | 5 |
|---|
Begitu juga dengan kotak III dan kotak IV ada 5 pilihan angka masing-masing. Banyaknya plat nomor plat nomor.
Jadi, banyaknya plat nomor yang bisa dibuat adalah 625 plat nomor.
Contoh soal gabungan aturan perkalian dan penjumlahan
Dari Kota A menuju kota D dapat melalui beberapa jalur pada gambar di bawah ini.
Berapa banyak kemungkinan jalur yang dapat dilalui dari Kota A ke Kota B?

Alternatif Penyelesaian ✍️
Untuk perjalanan dari kota A ke kota B bisa melalui kota C atau kota D. Beberapa jalur yang bisa ditempuh :
Jalur Pertama : jalurnya A - C - B
A - C ada 2 jalan dan C - B ada 3 jalan,
toal jalur pertama
Jalur Kedua : jalurnya A - D - B
A - D ada 3 jalan dan D - B ada 4 jalan,
total jalur kedua
Keseluruhan jalur yang ditempuh adalah melalui jalur pertama atau jalur kedua sehingga bisa menggunakan aturan penjumlahan.
Total jalur = jalur pertama jalur kedua = .
Jadi, banyak kemungkinan jalur yang ditempuh dari A ke B ada 18 jalur.
Notasi Faktorial
Untuk bilangan asli, Notasi atau bentuk faktorial bilangan didefinisikan sebagai berikut Cara penghitungannya :
dibaca “ faktorial”.
Pendifinisian faktorial hanya berlaku untuk bilangan asli. Untuk n=0 didefinisikan sendiri yaitu
Contoh soal faktorial :
Tentukan nilai faktorial berikut ini,
- 5!
- 3!
- 6!
Alternatif Penyelesaian ✍️
Aturan penjumlahan, aturan perkalian dan notasi faktorial ini nanti akan kita gunakan dalam kaidah pencacahan yang lainnya ya misalkan saja permutasi dan kombinasi, jadi pahami materi ini dengan baik..

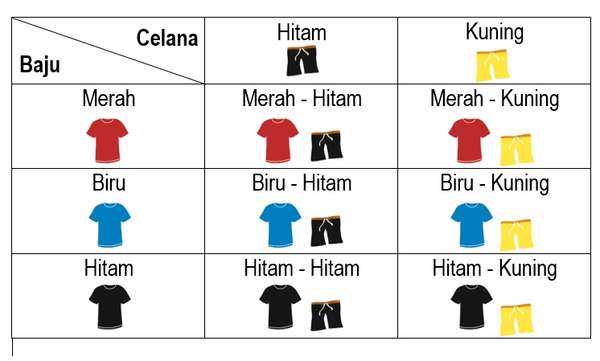 Berdasarkan tabel di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.
Berdasarkan tabel di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.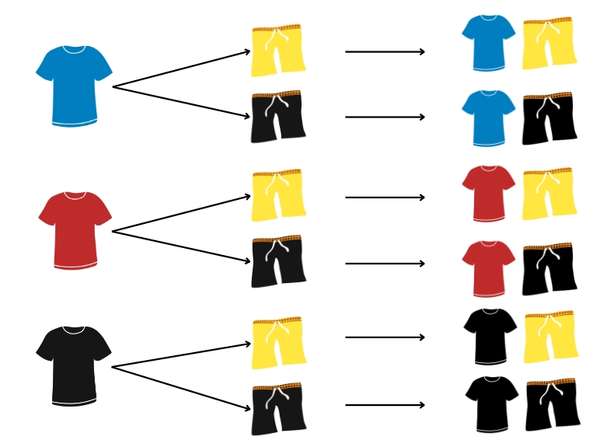 Berdasarkan diagram pohon di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.
Berdasarkan diagram pohon di atas terdapat enam variasi pasang baju dan celana yaitu merah-hitam, merah-kuning, biru-hitam, biru-kuning, hitam-hitam, dan hitam-kuning.