Pelajari Kaidah Pencacahan! Khususnya Aturan Pemutasi dan Kombinasi, Rumus, Contoh Soal, dan Perbedaannya! Baca selengkapnya di sini!

Hai Sobat SInmat!, pada kesempatan ini kita akan belajar tentang rumus permutasi dan kombinasi serta perbedaannya. Sebelum belajar tentang lebih lanjut, kita harus menguasai dulu yang namanya “kaidah pencacahan”. Kaidah pencacahan adalah cara menentukan banyaknya susunan atau cara pada suatu kejadian atau percobaan. Silakan pelajari aturan perkalian dan aturan penjumlahan↝ terlebih dahulu ya.

Agar lebih mudah memahami permutasi dan kombinasi, Perhatikan permasalahan berikut ya!

Permasalahan 1!

Permasalahan 2!

Dari kedua permasalahan di atas, ada perbedaan dalam susunan antara keduanya. Mari kita cermati!

  • Dari permasalahan 1 misalkan yang kita ambil adalah Andi, Budi, dan Caca. Maka susunan untuk ketua, sekretaris dan bendahara bisa kita bolak balik ya. Dan susunannya berbeda.

    Misalkan:

    susunan 1 Ketua, Sekretaris, dan Bendahara urutannya Andi, Budi, dan Caca. Susunan akan berbeda jika

    susunan 2 Ketua, Sekretaris, dan Bendahara urutannya Andi, Caca, dan Budi.

    dst

  • dari permasalahan 2 misalkan yang diambil adalah Andi, Budi, dan Caca. maka susunannya akan tetap sama walauppun urutan orangnya berbeda misalkan Andi, Budi, Caca maka akan tetap sama urutannya (1 tim) itu Budi, Andi, Caca.

Jelas ya perbedaannya, kalau poin pertama itu memperhatikan urutan. Sedangkan, poin kedua tidak memperhatikan urutannya.

Nah, keduanya bisa disebut dengan Permutasi dan kombinasi. Mari kita bahas satu persatu lebih mendalam ya.

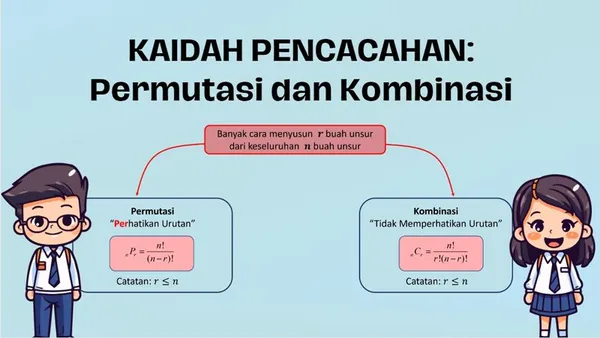
Perbedaan Permutasi dan Kombinasi

Permutasi dan kombinasi akan sering kamu gunakan ya sob, terutama dalam konsep peluang yang akan dipelajari selanjutnya. Perbedaannya yaitu:

Contoh:

1. Permutasi

Misalkan kita memilih dua orang yang akan menjadi ketua dan bendahara dari 4 orang A, B, C, dan D dalam suatu kelompok.

Karena pada permutasi harus memperhatikan urutan, maka susunan yang bisa kita peroleh dari kejadian di atas adalah A-B, A-C, A-D, B-A, B-C, B-D, C-A, C-B, C,D, D-A, D-B, D-C. Jadi, ada 12 susunan yang bisa kita peroleh dari pemilihan ketua dan sekretaris.

Perhatikan bahwa jika si A menjadi ketua dan si B menjadi bendahara maka susunan ini akan berbeda dengan si B menjadi ketua dan si A menjadi bendahara, atau secara singkat “URUTAN” sangat mempengaruhi sehingga AB $ \neq $ B pada permutasi.

2. Kombinasi

Misalkan, suatu kelompok memiliki 4 orang anggota, yaitu A, B, C, dan D. Seorang guru harus memilih 2 orang anggota untuk mengikuti lomba matematika. Tentukan ada berapa kombinasi yang digunakan untuk mengambil dua orang dari tiga anggota yang tersedia!

Kombinasi adalah permutasi tanpa memperhatikan nilai acak. Karena pada kombinasi tidak memperhatikan urutan, jadi cara yang bisa diambil dari kejadian di atas adalah A-B, A-C, A-D B-C, B-D, dan C-D. Dengan begitu, ada 6 kombinasi cara untuk mengambil dua orang dari tiga anggota untuk menjadi peserta lomba vokal.

Rumus dan Contoh Permutasi

Permutasi adalah cara penyusunan suatu percobaan atau suatu kejadian yang memperhatikan “URUTAN”. Contoh-contoh kejadian yang merupakan permutasi atau kejadian yang memperhatikan “URUTAN” yaitu pemilihan kepengurusan, penyusunan cara duduk, posisi dalam berfoto, menyusun angka, menusun plat nomor, dan pemilihan juara dalam lomba.

1. Permutasi dengan unsur yang berbeda

Permutasi dengan unsur yang berbeda digunakan saat unsur/objek yang tersedia semuanya berbeda. Banyak permutasi $r$ dari $n$ unsur yang berbeda dinotasikan dengan $_nP_r$ atau $P_r^n$ atau $P(n, r)$. Rumus permutasi sebagai berikut:

catatan: ingat faktorial di materi sebelumnya Notasi Faktorial↝

$n!=n\times (n-1) \times (n-2)\times … \times 3 \times 2 \times 1$

contoh: $5!= 5\times 4 \times 3 \times 2 \times 1 = 120 $

Contoh Soal Permutasi Unsur yang berbeda

  1. Dalam suatu organisasi akan dipilih pengurus sebagai ketua, sekretaris, dan bendahara dari 8 calon yang memenuhi kriteria. Banyak susunan pengurus yang mungkin dari 8 calon tersebut adalah …

    1. 24
    2. 56
    3. 336
    4. 343
    5. 512

    Alternatif Penyelesaian ✍️

    banyak susunan pengurus yang mungkin adalah $P_3^8$ $$\begin{align*} P_3^8&=\frac{8!}{(8-3)!}\\ &=\frac{8!}{5!} \\ &= \frac{ 8 \cdot 7 \cdot 6 \cdot \cancel{5!}}{\cancel{5!}} \\ &= 8\cdot 7 \cdot 6 \\ &=336 \end{align*}$$ Jadi, banyak susunan pengurus yang mungkin 336. C 😄

2. Permutasi dengan unsur yang sama

Permutasi dengan unsur yang sama digunakan untuk mencari banyak susunan yang mungkin muncul jika diantara unsur yang tersedia ada unsur yang sama. Banyak permutasi $n$ unsur yang memuat $r_1, r_2, r_3,…,r_n$ dinotasikan dengan $n P{r_1, r_2,…,r_n}$. Rumus permutasi dengan unsur yang sama sebagai berikut:

Contoh Soal Permutasi Unsur yang sama

  1. Banyak susunan kata yang dapat di bentuk dari kata ”MATEMATIKA” adalah….

    1. 12.150 kata
    2. 15.120 kata
    3. 150.120 kata
    4. 151.200 kata
    5. 152.100 kata

    Alternatif Penyelesaian ✍️

    Perhatikan huruf pada kata MATEMATIKA! ada huruf yang sama kan. banyak huruf masing-masing M=2, A=3, T=2, E=1, I=1, K=1

    banyak susunan kata yang dapat dibentuk adalah permutasi banyak huruf dari kata “MATEMATIKA” dengan huruf-huruf yang sama atau ${10} P{2,3,2}$

    $$\begin{align*} _{10} P_{2,3,2}&=\frac{10!}{2!\cdot 3! \cdot 2!}\\ &=\frac{10\cdot 9 \cdot 8 \cdot 7 \cdot 6\cdot 5\cdot 4\cdot \cancel {3!} }{2\cdot \cancel{3!} \cdot 2} \\ &=\frac{10\cdot 9 \cdot 8 \cdot 7 \cdot 6\cdot 5\cdot 4 }{4} \\ &= 10\cdot 9 \cdot 8 \cdot 7 \cdot 6\cdot 5 \\ &= 151.200 \end{align*}$$ Jadi, Banyak susunan kata yang dapat di bentuk dari kata ”MATEMATIKA” adalah 151.200. D 😄

3. Permutasi Siklis

Permutasi Siklis digunakan untuk menyusun n unsur berbeda secara melingkar atau mengelilingi daerah tertutup. Banyaknya permutasi r dari n unsur yang berbeda dinotasikan dengan $_nP _{(siklis)}$ atau $P_s (n)$.

Contoh Soal Permutasi Siklis

  1. Enam orang manager perusahaan duduk mengelilingi sebuah meja berbentuk melingkar untuk mengadakan rapat. Berapa banyak cara mereka dapat duduk mengelilingi meja rapat tersebut dengan urutan yang berbeda?

    Alternatif Penyelesaian ✍️

    Banyaknya cara agar 6 orang manager dapat duduk mengelilingi meja rapat sama dengan permutasi melingkar dari 6 unsur, yaitu
    $$\begin{align*}P_s (6) &= (6 – 1)! = 5!\\ & = 5 \times 4 \times 3 \times 2 \times 1 = 120 \end{align*}$$

    Jadi, banyak cara 6 orang manager perusahaan dapat duduk mengelilingi meja rapat tersebut dengan urutan yang berbeda adalah 120 cara.

  2. Satu keluarga terdiri dari ayah, ibu, dan 4 orang anaknya. Mereka duduk di meja makan yang bentuknya melingkar. Ada berapa cara anggota keluarga tersebut duduk mengelilingi meja jika ayah dan ibu selalu duduk berdampingan?

    Alternatif Penyelesaian ✍️

    • Syarat khusus, ayah dan ibu selalu duduk berdampingan. Posisinya dapat dipertukarkan sebanyak $2! = 2$ cara.
    • Ayah dan ibu selalu duduk berdampingan, sehingga posisi ini diblok dan dianggap 1 unsur. Blok (ayah dan ibu) dan 4 orang anaknya menjadi 5 unsur yang duduk melingkar, sehingga dengan permutasi siklik diperoleh: $$\begin{align*}P_s (5) &= (5 – 1)! = 4!\\ & = 4 \times 3 \times 2 \times 1 = 120 \end{align*}$$
    • Dengan Aturan perkalian diperoleh banyak cara anggota keluarga duduk mengelilingi meja jika ayah dan ibu selalu duduk berdampingan adalah $2 \times 24 = 48$ cara.

Rumus dan Contoh Kombinasi

Permutasi adalah banyak cara yang mungkin untuk memilih sekumpulan objek. Apa bedanya dengan kombinasi? Pada permutasi, susunan objek dipertimbangkan. Sementara pada kombinasi, susunan objek tidak lagi dipertimbangan (“TIDAK MEMPERHATIKAN URUTAN”),