Kedudukan Titik Terhadap Lingkaran

Pada materi sebelumnya kita sudah belajar tentang persamaan lingkaran. Selanjutnya kita akan belajar tentang kedudukan titik terhadap lingkaran.

Pada materi sebelumnya kita sudah belajar tentang persamaan lingkaran. Selanjutnya kita akan belajar tentang kedudukan titik terhadap lingkaran. Kita mulai dari kedudukan titik terhadap lingkaran. Jika titik $P(x_1,y_1)$ sembarang dan L adalah lingkaran dengan jari-jari $r$ maka ada tiga posisi titik $P$ terhadap lingkaran L yaitu

1. Titik P terletak pada lingkaran
2. Titik P di dalam lingkaran dan
3. Titik P diluar lingkaran

Untuk memahami materi ini perlu diingat tentang persamaan lingkaran yaitu:

1. persamaan lingkaran dengan pusatnya O(0,0) dan jari-jari r maka persamaannya adalah $x^2+y^2=r^2$
2. persamaan baku lingkaran yaitu jika pusatnya P(a,b) dan jari-jari r maka persamaannya adalah $(x-a)^2+(y-b)^2=r^2$
3. persamaan umum lingkaran yaitu $x^2+y^2+Ax+By+C=0$ dengan pusat $P(-\frac{1}{2}A,-\frac{1}{2}B)$ dan jari-jari $r=\sqrt{(\frac{1}{2}A)^2+(\frac{1}{2}B)^2-C}$

Kedudukan Titik Terhadap Lingkaran

1. Titik di dalam lingkaran

Perhatikan gambar berikut 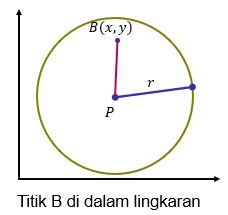misalkan titik $B(𝑥, 𝑦)$ terletak di dalam lingkaran yang berjari-jari 𝑟 dengan pusat P. Maka panjang $PB<r$ oleh karena itu

• jika pusat $O(0,0)$ maka $x^2+y^2<r^2$
• jika pusat $P(a,b)$ atau persamaan baku lingkaran maka $(x-a)^2+(y-b)^2<r^2$
• pada persamaan umum lingkaran $x^2+y^2+Ax+By+C<0$

2. Titik pada lingkaran

Perhatikan gambar berikut 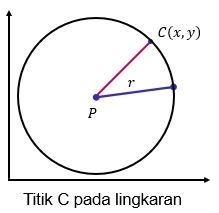misalkan titik $C(𝑥, 𝑦)$ terletak tepat pada lingkaran yang berjari-jari 𝑟 dengan pusat P. Maka panjang $PC=r$ oleh karena itu

• jika pusat $O(0,0)$ maka $x^2+y^2=r^2$
• jika pusat $P(a,b)$ atau persamaan baku lingkaran maka $(x-a)^2+(y-b)^2=r^2$
• pada persamaan umum lingkaran $x^2+y^2+Ax+By+C=0$

3. Titik di luar lingkaran

Perhatikan gambar berikut 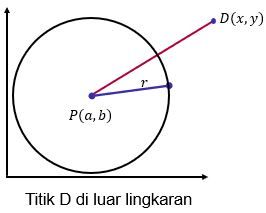misalkan titik $D(𝑥, 𝑦)$ terletak di luar lingkaran yang berjari-jari 𝑟 dengan pusat P. Maka panjang $PD>r$ oleh karena itu

• jika pusat $O(0,0)$ maka $x^2+y^2>r^2$
• jika pusat $P(a,b)$ atau persamaan baku lingkaran maka $(x-a)^2+(y-b)^2>r^2$
• pada persamaan umum lingkaran $x^2+y^2+Ax+By+C>0$

Contoh 1

Tentukan kedudukan titik 𝐴(−3,5), 𝐵(7,6), dan 𝐶(1,−2) terhadap lingkaran $𝑥^2+𝑦^2=34$.

Pembahasan

Substitusi titik 𝐴, 𝐵, dan 𝐶 ke pers. lingkaran $𝑥^2+𝑦^2$ (ruas kiri), kemudian membandingkan dengan nilai $𝑟^2=34$ (di ruas kanan).

• $𝐴(−3,5)=𝐴(𝑥_𝑎, 𝑦_𝑎)$ sehingga $𝑥_𝑎 = −3$ dan $𝑦_𝑎=5$ $$\begin{align*} 𝑥_𝑎^2+𝑦_𝑎^2&=(−3)^2+5^2\\𝑥_𝑎^2+𝑦_𝑎^2&=9+25\\𝑥_𝑎^2+𝑦_𝑎^2&=34=r^2 \end{align*}$$ Karena $34=r^2$ Berarti titik 𝐴(−3, 5) terletak pada lingkaran.
• $𝐵(7,6)=𝐵(𝑥_𝑏, 𝑦_𝑏)$ sehingga $𝑥_𝑏=7$ dan $𝑦_𝑏=6$ $$\begin{align*} 𝑥_𝑏^2+𝑦_𝑏^2&=7^2+6^2\\𝑥_𝑏^2+𝑦_𝑏^2&=49+36\\𝑥_𝑎^2+𝑦_𝑎^2&=75>r^2 \end{align*}$$ Karena $75>r^2$ Berarti titik 𝐵(7,6) terletak diluar lingkaran.
• $𝐶(1,−2)=𝐶(𝑥_𝑐, 𝑦_𝑐)$ sehingga $𝑥_𝑐=1$ dan $𝑦_𝑐=−2$ $$\begin{align*} 𝑥_𝑐^2+𝑦_𝑐^2&=1^2+(−2)^2\\𝑥_𝑐^2+𝑦_𝑐^2&=1+4\\𝑥_𝑎^2+𝑦_𝑎^2&=5<r^2 \end{align*}$$ Karena $5<r^2$ Berarti titik 𝐶(1, −2) terletak di dalam lingkaran.

Contoh 2

Tentukan kedudukan titik 𝐴(7, 5) terhadap lingkaran berpusat di titik (1, 3) dengan jari-jari 5.

Pembahasan
menentukan persamaan lingkaran yang berpusat di titik $𝑃(𝑎, 𝑏)$ dan memiliki jari-jari 𝑟 adalah $(𝑥−𝑎)^2+(𝑦−𝑏)^2=𝑟^2$.
Titik Pusat (1,3) dan jari $𝑟=5$ $$\begin{align*} (𝑥−1)^2+(𝑦−3)^2=5^2\\(𝑥−1)^2+(𝑦−3)^2=25 \end{align*}$$ Substitusi titik $𝐴(7,5)$ ke pers. lingkaran (ruas kiri), kemudian membandingkan dengan nilai $𝑟^2=25$ (di ruas kanan). $$\begin{align*} (𝑥_𝑎−𝑎)^2+(𝑦_𝑎−𝑏)^2&=(7−1)^2+(5−3)^2\\&=6^2+2^2\\&=36+4\\&=40\rightarrow 40>r^2 \end{align*}$$ Karena $40>r^2$, berarti titik $𝐴(7,5)$ terletak di luar lingkaran.

Contoh 3

Tentukan kedudukan titik $𝑃(1,2)$ terhadap lingkaran $𝑥^2+𝑦^2–8𝑥+12𝑦+36=0$.

Pembahasan
substitusikan titik $𝑃(1, 2)$ kedalam $𝑥^2+𝑦^2–8𝑥+12𝑦+36$ kemudian bandingkan dengan 0.
$$\begin{align*} 𝑥^2+𝑦^2–8𝑥+12𝑦+36&=1^2+2^2–8(1)+12(2)+36\\&=1+4-8+24+36\\&=57\rightarrow 57>0 \end{align*}$$ Karena $57>0$, berarti titik $𝑃(1, 2)$ terletak di luar lingkaran.

Contoh 4

Jika titik (1, 3) terletak pada lingkaran $3𝑥^2+3𝑦^2+𝑎𝑥–6𝑦–9=0$, tentukan:

1. nilai a
2. pusat dan jari-jari lingkaran.

Alternatif Penyelesaian

1. Titik (1, 3) terletak pada lingkaran $3𝑥^2+3𝑦^2+𝑎𝑥–6𝑦–9=0$ sehingga $$\begin{align*} 3(1)^2+3(3)^2+𝑎(1)–6(3)–9&=0\\3+27+𝑎–18–9&=0\\𝑎+3&=0\\ a&=-3 \end{align*}$$
2. Pers. lingkaran $3𝑥^2+3𝑦^2−3𝑥–6𝑦–9=0$ berarti persamaan umum lingkarannya $𝑥^2+𝑦^2−𝑥–2𝑦–3=0$
   Diperoleh $𝐴=−1, 𝐵=−2, 𝐶=−3$
   Pusatnya adalah $(−\frac{1}{2}A,−\frac{1}{2}B)=(−\frac{1}{2}(-1),−\frac{1}{2}(-2))=(\frac{1}{2},1)$
   Jari-jari $r=\sqrt{a^2+b^2-C}$ $$\begin{align*} r&=\sqrt{(\frac{1}{2})^2+1^2−(−3)}\\&=\sqrt{\frac{1}{4}+1+3)}\\&=\sqrt{\frac{17}{4}}\\&=\frac{1}{2}\sqrt{17} \end{align*}$$