Temukan penjelasan sederhana tentang limit fungsi dalam matematika. Lengkap dengan contoh soal dan visualisasi yang mudah dipahami dalam pelajaran matematika SMA
Pernahkah kamu bertanya-tanya, “Apa itu limit fungsi dan mengapa kita harus mempelajarinya?” Konsep limit mungkin terdengar asing dan rumit pada awalnya, namun sebenarnya sangat penting dalam matematika. Limit adalah konsep dasar yang menjadi fondasi untuk memahami konsep-konsep lanjutan seperti turunan dan integral.
Kita sering mendengar kata mendekati, misalnya, kecepatan mobil itu mendekati 160 km/jam.. Nah kata mendekati ini dalam matematika disebut dengan limit.
Dalam artikel ini, kita akan mempelajari limit fungsi yang biasa di pelajari pada jenjang SMA. Limit fungsi yang kita pelajari mengenai limit fungsi aljabar dan limit fungsi trigonometri. Sebelum membahas lebih lanjut, kita akan mempelajari pengertian limit secara mendalam dan menentukan nilai limit terlebih dahulu.
Apa itu Limit Fungsi?
Secara sederhana, limit fungsi adalah nilai pendekatan di sekitar titik tertentu baik pendekatan dari kiri maupun pendekatan dari kanan titik tersebut. Bayangkan sebuah grafik fungsi. Saat kita mendekati titik tertentu pada grafik, nilai fungsi akan semakin mendekati suatu nilai tertentu. Nilai inilah yang disebut limit.
Bentuk umum Notasi Limit Fungsi
$$\lim \limits_{x\rightarrow a} f(x) = L$$
- $\lim$: Singkatan dari “limit”.
- $f(x)$: Fungsi yang sedang kita tinjau.
- $x \rightarrow a$: Artinya “x mendekati a”.
- $L$: Nilai yang didekati oleh f(x) ketika x mendekati a.
Cara Membaca notasi limit fungsi :
$ \displaystyle \lim_{x \to a } f(x) = L $ dibaca limit fungsi $ f(x) $ untuk $ x $ mendekati $ a $ sama dengan $ L $ .
Untuk lebih jelasnya perhatikan ilustrasi berikut :
Misalkan terdapat suatu fungsi $𝑓(𝑥) = x+2$. Tentukan nilai $\lim\limits_{x \to 2} f(x) $ jika ada !
Untuk menentukan limit fungsi aljabar di $𝑥 \to 𝑎$ kita bisa menggunakan tabel seperti berikut.
Jika kita subtitusi nilai-nilai 𝑥 dari kiri maka nilainya akan mendekati 4, sedangkan jika kita subtitusi nilai-nilai x dari kanan maka nilainya akan mendekati 4 juga. Hal ini dapat dituliskan sebagai berikut.
$\lim\limits_{x \to 2^+}x+2=4 $ dan $\lim\limits_{x \to 2^-}x+2=4 $ maka $\lim\limits_{x \to 2}x+2=4 $.
Jika disajikan dalam grafik seperti berikut
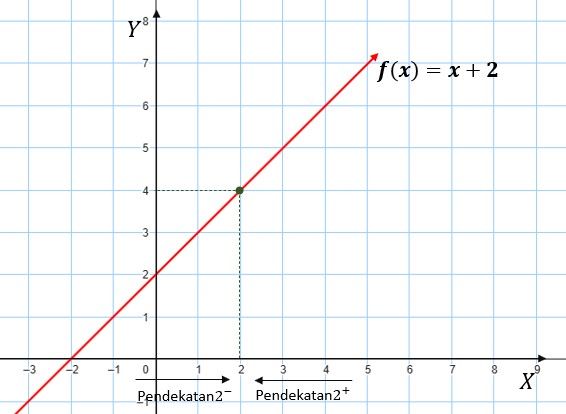
Jadi, nilai $\lim\limits_{x \to 2^+}x+2 $ adalah 4
Definisi Limit Fungsi
Secara matematis limit dapat didefinisikan sebagai berikut.
Misalkan $ f $ sebuah fungsi $ f : R \rightarrow R $ dan misalkan $ L $ dan $ a $ bilangan real.
$ \displaystyle \lim_{x \to a } f(x) = L $ jika dan hanya jika $ f(x) $ mendekati $ L $ untuk semua $ x $ mendekati $ a $ .
Cara Membaca notasi limit fungsi : $ \displaystyle \lim_{x \to a } f(x) = L $ dibaca limit fungsi $ f(x) $ untuk $ x $ mendekati $ a $ sama dengan $ L $ .
Syarat Limit Fungsi
Suatu limit dikatakan ada jika limit tersebut memiliki limit kiri dan limit kanan yang sama.
Jika fungsi 𝑓(𝑥) terdefinisi pada selang terbuka I, maka:
- $ \lim \limits_{x \to a} f(x) = L $ (ada) jika dan hanya jika $ \lim \limits_{x \to a^+} f(x) = L $ dan $ \lim \limits_{x \to a^-} f(x) = L $
- Jika $ \lim \limits_{x \to a^+} f(x) = L_1 $ dan $ \lim \limits_{x \to a^-} f(x) = L_2 $ dimana $𝐿_1 ≠ 𝐿_2$ maka $ \lim \limits_{x \to a} f(x) $ tidak ada
Biar makin paham simak contoh berikut ya…
Menentukan Nilai Limit Fungsi
Untuk menentukan nilai limit suatu fungsi, ada beberapa cara :
- Metode Numerik
- Subsitusi
- Pemfaktoran
- Kali sekawannya
- Menggunakan Turunan
Secara konsep dasar matematika, cara mengerjakan soal matematika yang ada limitnya, hanya tinggal mengganti/mensubtitusi variabel 𝒙 menjadi angka yang didekati oleh 𝑥 tersebut.
Contoh Soal 1
Tentukan limit f(x) untuk fungsi
$$f(x) = \begin{cases}2x^2 &\text{jika }x\leq 1 \\
2x-1 &\text{jika } x > 1
\end{cases}$$
untuk $ x $ mendekati 1 jika ada?
Alternatif Penyelesaian ✍️
Keterangan fungsi :
Jika nilai $ x \leq 1 $ maka berlaku $ f(x) = 2x^2 $
Jika nilai $ x > 1 $ maka berlaku $ f(x) = 3x + 1 $
Tabel pendekatan dari kiri dan dari kanan untuk $ x $ mendekati 1.
Analisa hasil limit kiri dan limit kanan. Tabel di atas menunjukkan : $ \lim \limits_{x \to 1^-} f(x) = 2 $ dan $ \lim \limits_{x \to 1^+} f(x) = 4 $ (limit kiri ≠ limit kanan), sehingga $ \lim \limits_{x \to 1} f(x) $ tidak ada.
Untuk lebih jelasnya perhatikan gambar berikut.
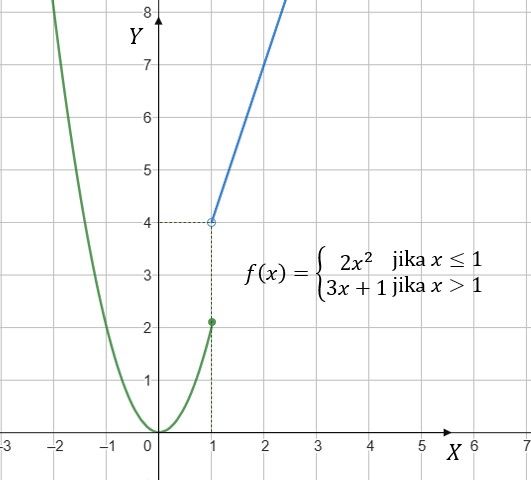
Jadi, fungsi $f(x) = \begin{cases}2x^2 &\text{jika }x\leq 1 \\ 2x-1 &\text{jika } x > 1 \end{cases}$ muntuk $ x $ mendekati 1 tidak mempunyai limit.
Contoh Soal 2
Diketahui $\lim\limits_{x \to 1} \frac{5x^3+7x^{14}+6}{8x^9+4x^7-6}$ Berapakah hasil nilai limit dari data diatas ?
Alternatif Penyelesaian ✍️
Pada limit diatas, untuk mencari hasil nilai limitnya, kalian hanya tinggal mensubtitusi atau mengganti variabel 𝑥 dengan angka 1, sehingga hasil limitnya menjadi $$\begin{align*}\lim\limits_{x \to 1} \frac{5x^3+7x^{14}+6}{8x^9+4x^7-6} &=\frac{5.1^3+7.1^{14}+6}{8.1^9+4.1^7-6} \\ &= \frac{5+7+6}{8+4-6} \\ &=\frac{18}{6} =3\end{align*}$$ Jadi, nilai limit tersebut adalah 3
Demikian artikel semoga kalian lebih mudah memahami konsep limit fungsi dan termotivasi untuk terus belajar matematika. Selanjutnya kita akan belajar tentang sifat-sifat limit fungsi.
Tetap semangat ya…