Apa itu matriks? Kali ini, kita akan membahas konsep matriks meliputi pengertian dan jenisnya yang dipelajari pada kelas XI Fase F. Simak baik-baik, ya!
Hai Sobat Sinmat, kali ini kita akan belajar tentang konsep matriks dan juga jenis-jenisnya. Matriks dalam matematika adalah susunan bilangan yang berbentuk persegi panjang yang disusun menurut baris dan kolom. Matriks akan dipelajari pada kelas XI atau fase F pada Kurikulum Merdeka ya. Harapannya kamu dapat menyatakan data dalam bentuk matriks.
Matriks dimanfaatkan di dalam menyelesaikan bermacam-macam permasalahan matematika, misalnya: untuk menemukan pemecahan masalah persamaan linear, transformasi linear. Sebagai gambaran awal mengenai matriks, sekarang coba cermati uraian berikut.
Diketahui harga tiket masuk suatu museum dapat dinyatakan sebagai tabel berikut:
Data tersebut, dapat disajikan kembali tanpa harus di dalam tabel, dengan cara menghilangkan kepala baris dan kepala kolom seperti berikut ini:
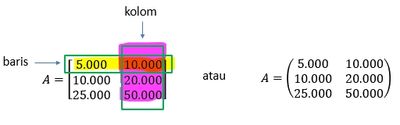
Bentuk penulisan tersebut, menunjukkan terdapat 3 baris dan 2 kolom. Urutan angka-angkanya sama dengan tabel. hanya keterangan baris dan kolomnya aja yang dihilangkan. Terus, angka-angka tersebut diberi tanda kurung di sisi kanan dan kirinya. Kalo dalam Matematika, bentuk tersebut dinamakan matriks.
Pengertian Matriks
Matriks adalah susunan bilangan berbentuk persegi atau persegi panjang yang diatur menurut baris dan kolom, dan ditempatkan dalam tanda kurung biasa atau kurung siku. Nah, tanda kurungnya ini bisa berupa kurung biasa “( )” atau kurung siku “[ ]”, ya
Matriks diberi nama dengan menggunakan huruf kapital, seperti $A, B,$ dan $C$.
Bentuk umum Matriks
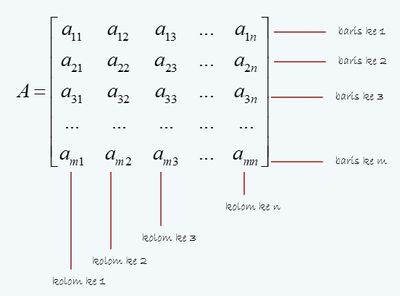Pada bentuk matriks tersebut, terlihat hal-hal sebagai berikut.
- Banyaknya baris dan kolom matriks $A$ berturut-turut adalah m dan n buah.
- $a_{11}, a_{12}, a_{13}, …, a_{mn}$ disebut dengan elemen-elemen matriks A, $a_{mn}$ = elemen $A$ pada baris ke-$m$, kolom ke-$n$.
Penamaan baris dan kolom dibuat urut, ya. Jadi, baris ke-1 dimulai dari atas, urut ke bawah. Sementara itu, kolom ke-1 dimulai dari kiri ke kanan.
Ordo dan Elemen Matriks
Ordo atau ukuran suatu matriks ditentukan oleh banyaknya baris dan banyaknya kolom.
Secara umum berlaku:
Jika matriks $A$ mempunyai $m$ baris dan $n$ kolom maka matriks $A$ berordo $m × n$ atau ordo matriks A adalah $m × n$, ditulis:
$A_{m×n}$ (dibaca: ”A m kali n”).
Masing-masing bilangan yang terdapat di dalam matriks disebut elemen matriks. Kalo matriks dinotasikan dengan huruf kapital, maka elemen-elemen matriks dinotasikan dengan huruf kecil dan diberi indeks yang menyatakan letak baris dan kolomnya.
sebagai contoh nih matriks A
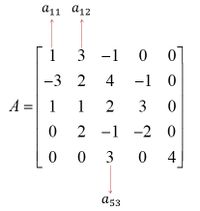
Pada matriks A di atas, jumlah barisnya kan ada 5 dan jumlah kolomnya juga ada 5, maka ordonya adalah $5 \times 5$, atau bisa kita tulis $A_{5×5}$. Lalu, untuk elemen-elemen matriks A bisa dinotasikan dengan $a_{mn}$, yang menyatakan elemen matriks $A$ pada baris ke-m dan kolom ke-m.
Untuk elemennya kita ambil contoh $a_{11}$, $a_{12}$, dan $a_{53}$, seperti pada gambar.
- $a_{11}$ menyatakan elemen matriks A pada baris ke-1 kolom ke-1, nilainya adalah 1.
- $a_{12}$ menyatakan elemen matriks A pada baris ke-1 kolom ke-2, nilainya adalah 3.
- $a_{53}$ menyatakan elemen matriks A pada baris ke-5 kolom ke-3, nilainya adalah 3.
Jenis-jenis Matriks
Selain punya ukuran (ordo), matriks juga terbagi menjadi beberapa bentuk yang mempunyai sifat khusus. Nah, beberapa jenis matriks khusus yang perlu kamu ketahui di antaranya sebagai berikut:
1. Matriks Baris
Matriks Baris yaitu matriks yang hanya mempunyai satu baris saja dan banyaknya kolom $n$, mempunyai ordo $1 \times n$
Contoh : $$𝑃_{1\times3}= \begin{pmatrix}1 \\ 2 \\ -3\end{pmatrix}$$
2. Matriks Kolom
Matriks Kolom yaitu matriks yang hanya mempunyai satu kolom saja dan banyaknya baris m, mempunyai ordo m x 1
contoh: $$𝑃_{3\times1}= \begin{bmatrix}1 & 2 & -3\end{bmatrix}$$
3. Matriks Persegi Panjang
Matriks Persegi Panjang yaitu matriks yang banyaknya baris tidak sama dengan banyaknya kolom, mempunyai ordo m x n
Contoh : $$R_{3\times2}= \begin{bmatrix}1 & 2 & -3 \\ -2 & 0 &2\end{bmatrix}$$
4. Matriks Persegi
Matriks Persegi atau Matriks Bujur sangkar, yaitu matriks yang mempunyai banyaknya baris sama dengan banyaknya kolom, mempunyai ordo n x n Contoh : $$S_{3\times3}= \begin{bmatrix}1 & 2 & -3 \\ -2 & 0 &2 \\ -1 & 0 &3\end{bmatrix}$$
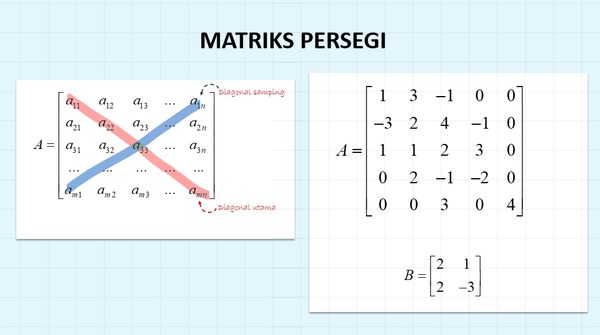
5. Matriks Diagonal
Matriks Diagonal, yaitu matriks persegi berordo n x n, dengan semua elemen di luar diagonal utamanya bernilai nol
6. Matriks Segitiga Atas
Matriks Segitiga Atas, yaitu matriks persegi n x n, dan semua elemen-elemen di bawah diagonal utamanya bernilai nol
7. Matriks Segitiga Bawah
Matriks Segitiga Bawah, yaitu matriks persegi n x n, dan semua elemen-elemen di atas diagonal utamanya bernilai nol
8 Matriks Identitas
Matriks identitas (matriks satuan), yaitu matriks diagonal dengan ordo n x n, dan semua elemen pada diagonal utamanya bernilai satu, dinotasikan dengan huruf “I”
Contoh : $$I= \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 &0 \\ 0 & 0 &1\end{bmatrix}$$ Elemen diagonal utamanya bernilai 1
9. Matriks Nol
Matriks Nol, yaitu matrik berordo m x n dengan semua elemennya bernilai nol Contoh : $$S_{3\times2}= \begin{bmatrix}0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}$$
Gimana, guys, udah paham dengan konsep matriks? Sebetulnya, matriks itu materi yang mudah lho, seru lagi! Matriks ini bisa digunakan untuk menyelesaikan masalah sistem persamaan yang memiliki lebih dari dua variabel dengan cepat. Dibandingkan kamu harus menggunakan metode substitusi atau eliminasi. Jadi, penting banget untuk memahami materi satu ini.
Sebagai latihan untuk lebih meningkatkan pemahaman tentang matriks, silakan Carilah 3 permasalahan nyata dalam sehari-hari kalian, kemudian buatlah:
- Bentuk matriks nya
- Ordo atau ukuran matriks