vektor adalah besaran yang selain mempunyai nilai kuantitatif (besar) juga mempunyai arah, misalnya besaran kecepatan, gaya, dan momen
Daftar Isi
1. Pengertian skalar dan vektor
Dalam kehidupan sehari-hari, kita banyak menjumpai besaran-besaran, seperti panjang sebuah tongkat, volume suatu kaleng, luas sebidang kebun, banyaknya muatan listrik, massa suatu benda dan sebagainya. Besaran-besaran itu biasanya dinyatakan dengan suatu bilangan yang disertai dengan satuan besaran tersebut. Besaran-besaran seperti itu, disebut skalar.
Apabila kita memindahkan atau menggeser sebuah benda (materi) yang berbentuk apa saja, maka perpindahan benda itu akan memenuhi dua unsur yaitu seberapa jauh kepindahannya dan ke arah mana benda itu berpindah. Kedua unsur yang memengaruhi perpindahan benda itu disebut sebagai besaran vektor. Jadi, vektor adalah besaran yang selain mempunyai nilai kuantitatif (besar) juga mempunyai arah, misalnya besaran kecepatan, gaya, dan momen.
Contoh:
Sebuah mobil melaju dengan kecepatan 100 km/jam ke arah barat. Peristiwa tersebut merupakan salah satu bentuk penggunaan vektor dalam kehidupan sehari-hari. Vektor yang digunakan mempunyai besar 100 km/jam dan melaju ke arah barat.
2. Menggambar dan menulis vektor
Notasi vektor dan teknik-teknik dengan menggunakan analisis vektor sangat berguna untuk menjelaskan hukum-hukum sains dan aplikasinya baik dalam bidang (dimensi dua = R2) maupun ruang (dimensi tiga = R3). Secara geometris, vektor dapat disajikan dengan ruas garis berarah. Panjang ruas garis menyatakan besar vektor dan anak panah menyatakan arah vektor. Dalam penyajiannya sebuah vektor biasa digambarkan sebagai segmen atau ruas garis yang berarah sebagai berikut :
Suatu vektor dapat diberi simbol dengan salah satu anggotanya sebagai wakil dari himpunan ruas garis. Vektor pada gambar diatas dapat diwakili oleh salah satu ruas garis, misalnya $\underline{a}$ atau $\overrightarrow{\text{AB}},\text{ }\overrightarrow{\text{CD}}\text{, }\overrightarrow{\text{EF}}$ atau lainnya. Dalam literatur terdapat beberapa simbol untuk wakil vektor, antara lain:
(1) dengan huruf kecil a, b, c, … (yang dicetak tebal) atau $\underline{a}$, $\underline{b}$, $\underline{c}$,…, atau $\overline{\text{a}},\text{ }\overline{\text{b}}\text{, }\overline{\text{c}}\text{, }…$
(2) dengan huruf besar, misalnya $\overrightarrow{\text{AB}}$atau $\underrightarrow{\text{AB}}$, $\overrightarrow{\text{PQ}}$atau $\underrightarrow{\text{PQ}}$, dan sebagainya. Anak panah yang menyertainya menyatakan arah, misalnya $\overrightarrow{\text{AB}}$ dimaksudkan sebagai wakil vektor dengan titik pangkal A dan bertitik ujung B.
Besar atau panjang sebuah vector $\overline{\text{a}}$ dapat dinyatakan dengan $\left| \overline{\text{a}} \right|$, sedangkan besar vector $\overrightarrow{AB}$dapat dinyatakan dengan $\left| \overrightarrow{\text{AB}} \right|$.
3. Ruang Vektor
Pada saat pertama kali ilmu vektor dikembangkan , hanya dikenal vektor-vektor di ${{R}^{2}}$ dan ${{R}^{3}}$ saja, tetapi dalam perkembangannya ternyata didapatkan permasalahan yang lebih kompleks sehingga dikembangkan vektor–vektor di ruang berdimensi 4 , 5 atau secara umum merupakan vektor-vektor di ${{R}^{n}}$ . Secara geometris memang vektor – vektor di ${{R}^{4}}$ dan seterusnya memang belum bisa digambarkan , tetapi dasar yang digunakan seperti operasi-operasi vektor masih sama seperti operasi pada vektor – vektor di ${{R}^{2}}$ dan ${{R}^{3}}$ . Orang yang pertama kali mempelajari vektor-vektor di Rn adalah Euclidis sehingga vektor–vektor yang berada di ${{R}^{n}}$ dikenal sebagai vektor Euclidis, sedangkan ruang vektornya disebut ruang–n Euclidis.
Pada materi ini yang kita pelajari adalah vektor di ${{R}^{2}}$ dan vektor di ${{R}^{3}}$. Vektor di ${{R}^{3}}$ adalah vektor yang terletak di ruang dimensi tiga atau vektor yang mempunyai tiga komponen yaitu x,y,z. Sedangkan, vektor di ${{R}^{2}}$ adalah vektor yang terletak di suatu bidang atau vektor yang hanya mempunyai dua komponen yaitu x dan y.
4. Vektor Nol
Vektor nol adalah vektor yang besar/panjangnya nol (titik awal dan titik ujungnya sama/berimpit) dan arahnya tak tentu seperti: $\overrightarrow{AA}=\overrightarrow{O},\overrightarrow{BB}=\overrightarrow{O}$. Pada sistem koordinat cartesius vektor nol digambarkan berupa titik. Di ruang dimensi dua vektor nol dilambangkan dengan $\overrightarrow{O}=\left( 0 0 \right)$
5. Vektor Negatif
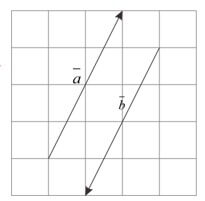
Vektor negatif dari $\overline{a}$ adalah vektor yang besarnya sama dengan vektor $\overline{a}$, tetapi arahnya berlawanan dan ditulis $-\overline{a}$. Perhatikan gambar di samping. Vektor $\overline{a}$ sejajar $\overline{b}$ dan sama panjang namun arahnya saling berlawanan maka $\overline{a}=-\overline{b}$.
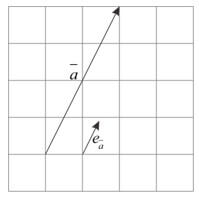
6. Vektor Satuan
Vektor satuan adalah vektor yang mempunyai panjang 1 satuan dan dinotasikan sebagai $e$. Vektor satuan dari vektor $\overline{a}$ didefinisikan vektor $\overline{a}$ dibagi dengan besar vektor $\overline{a}$ sendiri, yang dirumuskan dengan ${{e}_{\overline{a}}}=\frac{\overline{a}}{\left| \overline{a} \right|}=\frac{1}{\left| \overline{a} \right|}\overline{a}$
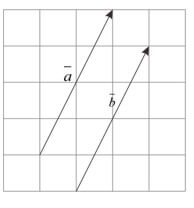
7. Kesamaan Dua Vektor
Dua buah vektor $\overline{a}$ dan $\overline{b}$ dikatakan sama apabila keduanya mempunyai besar (panjang) dan arah yang sama. Perhatikan gambar di samping. Terlihat $\overline{a}$ sejajar $\overline{b}$ dan besarnya sama. Diperoleh $\overline{a}=\overline{b}$.
