latihan soal pts atau asesmen sumatif pada kurikulum merdeka kelas x sma smk untuk menghadapi penilaian tengah semester

Sebentar lagi PTS nih atau penilaian tengah semester atau kalau di kurikulum merdeka namanya asessmen sumatif tengah semester…

Sudah siap belum menghadapi PTS? kali ini Sinmat akan berbagi beberapa soal matematika kelas X dengan materinya Fungsi Kuadrat dan Perbandingan Trigonometri. Nah bagi, yang belum tau materinya silahkan pelajari dulu Menentukan Akar Persamaan Kuadrat↝ , Menentuntukan Nilai Fungsi Kuadrat↝ , Menggambar Grafik Fungsi Kuadrat↝ , Menentukan Rumus Fungsi Kuadrat jika diketahui Grafik↝ , dan Perbandingan Trigonometri pada Segitiga Siku-siku↝

  1. Tentukan akar dari persamaan kuadrat $x^2-3x-18=0$!

    Alternatif Penyelesaian ✍️

    untuk menentukan akar persamaan kuadrat ada beberapa cara yaitu pemfaktoran, kuadrat sempurna, dan rumus ABC. Pilih yang menurut kamu paling mudah.

    Berikut cara pemfaktoran (berapa kali berapa yang hasilnya -18 dan berapa tambah berapa yang ditambah hasilnya -3) $$\begin{align*}x^2-3x-18=0\\x^2-6x+3x-18=0 \\ x(x-6)+3(x-6)=0 \\ (x+3)(x-6)=0\end{align*}$$

    $$x+3=0 \text{ atau } x-6=0 \\ x=-3 \text{ atau } x=6$$

    Jadi akar dari persamaan kuadrat $x^2-3x-18=0$ adalah $x=-3$ atau $x=6$

  2. Tentukan nilai dari fungsi kuadrat $f(x)=2x^2-3x-16$ untuk $x=-10$!

    Alternatif Penyelesaian ✍️

    semua $x$ diganti dengan 3 $$\begin{align*}f(x)&=2x^2-3x-16\\f(-10)&=(-10)^2-3(-10)-16\\&=100+30-16\\&=114\end{align*}$$

    Jadi, nilai dari $f(x)$ untuk $x = -100$ adalah $114$. 😄

  3. Gambarkan sketsa grafik fungsi kuadrat $f(x)=-x^2+4x+5$, dengan Langkah

    1. Menentukan sumbu simetri
    2. Menentukan titik puncak
    3. Menentukan titik potong terhadap sumbu x dan sumbu y (jika ada)

    Alternatif Penyelesaian ✍️

    Diketahui Persamaan fungsi kuadrat $f(x)=-x^{2}+4x+5$ diperoleh nilai $a=-1$, $b=4$, dan $c=5$

    1. Step 1. Menentukan persamaan sumbu simetri.

      Persamaan sumbu simetri:

      Substitusi $a=-1$, $b=4$ ke dalam $x=-\frac{b}{2a}$

      $$\begin{align*}x&=-\frac{b}{2a}\\ x&=-\frac{4}{2(-1)}\\x&=2\end{align*}$$

    2. Step 2. Menentukan Koordinat titik puncak

      Substitusi $x=2$ ke dalam fungsi kuadrat $f(x)=-x^{2}+4x+5$.

      $$\begin{align*}f(x)&=-x^{2}+4x+5\\ f(2)&=-(2)^{2}+4(2)+5\\ &=-4+8+5\\&=9\end{align*}$$

      Jadi, koordinat titik puncaknya (2, 9).

    3. Step 3. Menentukan titik potong terhadap sumbu X dan Y.

      • Grafik akan memotong sumbu X jika $y=0$.

        $y=f(x)=-x^{2}+4x+5$

        $$\begin{gather*}y=-x^{2}+4x+5 \\ 0=-x^{2}+4x+5 \\ x^{2}-4x-5=0\\(x-5)(x+1)=0 \\ x-5=0 \text{ atau } x+1=0 \\ x=5 \text{ atau } x=-1 \end{gather*}$$

        Jadi, titik potong terhadap sumbu X terletak pada koordinat (5, 0) dan (-1, 0).

      • Grafik akan memotong sumbu Y jika $x = 0$.

        $$\begin{align*}f(x)&=-x^{2}+4x+5 \\ f(0)&=-(0)^{2}+4(0)+5 \\ f(0)&=0 \end{align*}$$

        Jadi, titik potong terhadap sumbu Y terletak pada koordinat (0, 5).

    4. Step 4. Gambar sketsa grafik berdasarkan koordinat yang diperoleh.

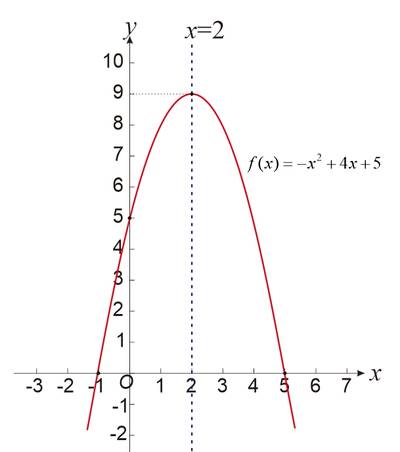
      Setelah menyelesaikan langkah ssebelumnya diperoleh titik-titik (2,9), (5,0), (-1,0), (0,5) dan sumbu simetrri $x=2$. Diperoleh gambar sketsa grafik fungsi kuadrat $f(x)=-x^{2}+4x+5$ seperti pada gambar di bawah ini.

      contoh soal sketsa grafik fungsi kuadrat

  4. Tentukan rumus fungsi kuadrat dari gambar grafik berikut Menentukan rumus fungsi kuadrat dari grafik

    Alternatif Penyelesaian ✍️

    • Dari gambar diketahui titik puncak : $(x_p,y_p) = (1,-8) $ dan titik lain $A(0,-6)$
    • Menyusun Fungsi Kuadrat yang diketahui titik puncaknya $$\begin{align*}y &= a(x-x_p)^2 + y_p \\y &= a(x-1)^2 -8 \end{align*}$$
    • Menentukan nilai $ a $ dengan substitusi titik A(0,-6) $$\begin{align*} (x,y)=(0,-6) \rightarrow y &= a(x-1)^2 -8 \\ -6 &= a(0-1)^2 - 8 \\ -6 &= a - 8 \\ a &= 2 \end{align*}$$
    • Substitusi nilai $ a = -2 $ ke pers awal $$\begin{align*} a = 2 \rightarrow y &= a(x-1)^2 -8 \\ y &= 2(x-1)^2 -8 \\ y &= 2(x^2-2x+1) - 8 \\ y &= 2x^2 -4x +2 - 8 \\ y &= x^2 - 4x -6 \end{align*}$$ Jadi fungsi kuadratnya adalah $ y = x^2 - 4x -6 $ 😄

  5. Diketahui segitiga siku-siku ABC dengan siku-siku di C. Jika Panjang AC= 3 cm dan BC = 4 cm, tentukan

    1. Gambar segitiga ABC
    2. Nilai sin A
    3. Nilai cos A
    4. Nilai tan A
    5. Nilai sin B
    6. Nilai cos B
    7. Nilai tan B

    Alternatif Penyelesaian ✍️

    • menggambar segitiga siku-siku Soal 5 Perbandingan Trigonometri
    • mencari panjang sisi AB atau sisi miring dengan pythagoras.
      $$\begin{align*} AB&=\sqrt{AC^2+BC^2}\\ &=\sqrt{3^2+4^2}\\ &=\sqrt{9+16}\\ &=\sqrt{25}\\ AB&=5 \end{align*}$$
    • mencari nilai $\sin A, \cos A, \tan A$ $$\sin A=\frac{de}{mi}=\frac{BC}{AB}=\frac{4}{5}$$ $$\cos A=\frac{sa}{mi}=\frac{AC}{AB}=\frac{3}{5}$$ $$\tan A=\frac{de}{sa}=\frac{BC}{AC}=\frac{4}{3}$$