Di Kelas 10 X Fase E Kurikulum Merdeka dipelajari bagaimana menentukan fungsi kuadrat jika grafiknya diketahui. Bagaimana caranya? simak disini!

Daftar Isi

Jika ada grafik berbentuk parabola dan kamu diminta menentukan atau menyusun fungsinya, bagaimana cara menentukannya? Sobat Sinmat, setelah sebelumnya kita belajar cara menggambar sketsa grafik fungsi kuadrat↝ dan bentuk umum fungsi kuadrat↝ kali ini kita akan belajar bagaimana menyusun dan menentukan fungsi kuadrat berdasarkan grafik yang diketahui atau berdasarkan titik-titik yang diketahui.

Mari kita ingat sebentar bentuk umum fungsi kuadrat dan ciri-ciri grafiknya

Bentuk Umum Fungsi Kuadrat

Fungsi kuadrat merupakan fungsi polinomial dengan pangkat pada variabel tertingginya adalah dua.

Bentuk umum dari fungsi kuadrat yaitu $$f(x) = ax^2 + bx + c$$ dengan keterangan sebagai berikut.

Keterangan:

$a$ = koefisien dari $x^2$, di mana $a ≠ 0$

$b$ = koefisien dari $x$

$c$ = konstanta

Ciri-Ciri Grafik Fungsi Kuadrat

Grafik fungsi kuadrat memiliki beberapa ciri, di antaranya yaitu:

  1. Berbentuk parabola
  2. Grafiknya simetris
  3. Hanya memiliki titik maksimum saja atau titik minimum saja, namun tidak keduanya (1 titik puncak atau 1 titik balik)

Nah, dari grafik fungsi kuadrat, kita bisa merumuskan fungsi kuadratnya. Yuk, kita masuk ke pembahasan utama yaitu merumuskan fungsi kuadrat berdasarkan grafik!

Cara Menentukan Fungsi Kuadrat Berdasarkan Grafik

Sebelum menentukan fungsi kuadrat berdasarkan grafik, kita harus lihat dulu nih, titik-titik apa yang diketahui pada grafik tersebut, karena rumus yang akan kita pakai tergantung dari nilai apa yang diketahui pada grafik. Biasanya yang diketahui adalah titik puncaknya, titik potong terhadap sumbu X, dan tiga titik sembarang yang dilalui oleh grafik.

Ada tiga rumus dasar yang bisa kita pakai dalam menyusun fungsi kuadrat

  1. Jika pada grafik diketahui titik puncaknya $(x_p , y_p) $ dan 1 titik lain sembarang

    Rumus : $ y = a(x-x_p)^2 + y_p $

    dengan nilai $ a $ diperoleh dari titik lain yang diketahui.

  2. Jika grafik memotong sumbu X di dua titik $ x_1 $ dan $ x_2 $ yaitu $(x_1,0) $ dan $(x_2,0)$ dan diketahui 1 titik lain sembarang

    Rumus : $ y = a(x-x_1)(x-x_2) $

    dengan nilai $ a $ diperoleh dari titik lain yang diketahui.

  3. Jika grafik melalui tiga titik sembarang selain titik-titik yang telah disebutkan di atas

    Cara : Untuk menentukan fungsi kuadratnya, substitusikan ketiga titik yang diketahui ke bentuk umum Fungsi Kuadrat $ y = ax^2+bx+c $ , lalu tentukan nilai $ a , b , $ dan $ c $ dengan menggunakan penyelesaian SPLTV.

Contoh Soal menentukan Fungsi Kuadrat berdasar grafiknya

Contoh Soal 1

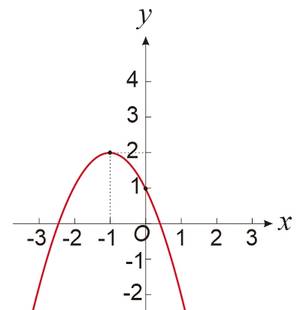
Tentukan fungsi kuadrat yang memiliki titik puncak $(-1,2)$ dan melalui titik $(0,1)$ ? Soal grafik fungsi kuadrat jika diketahui titik puncak dan 1 titik lain

Alternatif Penyelesaian ✍️

  • Diketahui titik puncak : $(x_p,y_p) = (-1,2) $ dan titik lain $(0,1)$
  • Menyusun Fungsi Kuadrat yang diketahui titik puncaknya $$\begin{align*}y &= a(x-x_p)^2 + y_p \\y &= a(x-(-1))^2 + 2 \\y &= a(x+1)^2 + 2 \end{align*}$$
  • Menentukan nilai $ a $ dengan substitusi titik (0,1) $$\begin{align*} (x,y)=(0,1) \rightarrow y &= a(x+1)^2 + 2 \\ 1 &= a(0+1)^2 + 2 \\ 1 &= a + 2 \\ a &= -1 \end{align*}$$
  • Substitusi nilai $ a = -1 $ $$\begin{align*} a = -1 \rightarrow y &= a(x+1)^2 + 2 \\ y &= (-1).(x+1)^2 + 2 \\ y &= (-1).(x^2+2x+1) + 2 \\ y &= -x^2 -2x -1 + 2 \\ y &= -x^2 -2x + 1 \end{align*}$$ Jadi fungsi kuadratnya adalah $ y = -x^2 -2x + 1 $ 😄

Contoh Soal 2

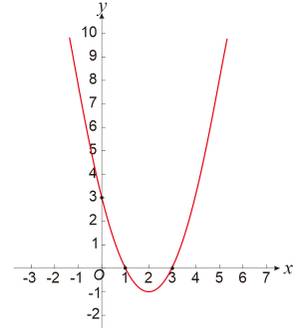
Tentukan fungsi kuadrat dari grafik seperti di bawah ini ? Grafik fungsi kuadrat dikethui 2 titik potong sumbu x

Alternatif Penyelesaian ✍️

  • Grafik memotong sumbu X di (1,0) dan (3,0), artinya $ x_1 = 1 $ dan $ x_2 = 3 $, serta melalui titik (0,3).
  • Menyusun Fungsi Kuadrat : $ y = a(x-x_1)(x-x_2) $ $$\begin{align*}y &= a(x-x_1)(x-x_2) \\y &= a(x-1)(x-3) \end{align*}$$
  • Menentukan nilai $ a $ dengan substitusi titik (0,3) $$\begin{align*} (x,y)=(0,3) \rightarrow y &= a(x-1)(x-3) \\ 3 &= a(0-1)(0-3) \\ 3 &= 3a \\ a &= \frac{3}{3} =1 \end{align*}$$
  • Substitusi nilai $ a $ $$\begin{align*} a=1 \rightarrow y &= a(x-1)(x-3) \\ y &= 1(x-1)(x-3) \\ y &= x^2 - 4x + 3 \end{align*}$$ Jadi fungsi kuadratnya adalah $ y =x^2 - 4x + 3 $ 😄

Contoh Soal 3

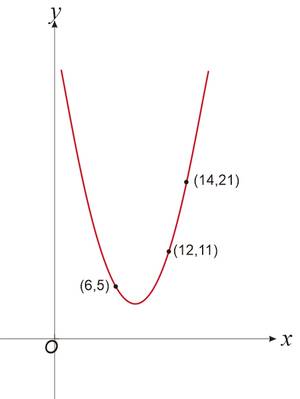
Tentukan fungsi kuadrat dari grafik di bawah ini ? Grafik fungsi kuadrat jika diketahui 3 titik sebarang

Alternatif Penyelesaian ✍️

  • Grafik melalui titik (6,5), (12,11), dan (14,21). Karena titik yang diketahui bukan titik puncak atau bukan titik potong sumbu X, maka kita gunakan cara ketiga yaitu substitusi semua titik tersebut ke bentuk umum Fungsi Kuadrat : $ y = ax^2 + bx + c $

  • Substitusi semua titik ke $ y = ax^2 + bx + c $ $$\begin{align*} (x,y)=(6,5) \rightarrow &5 = a.6^2 + b.6 + c & \\ &36a+6b+c = 5 &\text{ …pers(i)} \\ (x,y)=(12,11) \rightarrow &11 = a.(12)^2 + b.12 + c & \\ &144a+12b+c = 11 &\text{ …pers(ii)} \\ (x,y)=(14,21) \rightarrow &21 = a.(14)^2 + 14.6 + c & \\ &196a+14b+c = 21 &\text{ …pers(iii)} \end{align*}$$

  • Eliminasi dan substitusi ketiga persamaan di atas untuk menentukan nilai $ a, b, $ dan $ c $ .

    • Eliminasi pers(i) dan pers(ii) : $$\begin{array}{cc} 144a+12b+c = 11 & \\ 36a+6b+c = 5 & - \\ \hline 108a+6b = 6 & \text{… pers (iv)} \end{array} $$
    • Eliminasi pers(i) dan pers(iii) : $$\begin{array}{cc} 196a+14b+c = 21 & \\ 36a+6b+c = 5 & - \\ \hline 160a+8b = 16 & \text{… pers (v)} \end{array} $$
    • Eliminasi variabel $ b $ dari pers(iv) dan pers(v) $$\begin{array}{c|c|cc} 160a+8b = 16 & \times \frac{1}{8} & 20a+b=2 & \\ 108a+6b = 6 & \times \frac{1}{6} & 18a+b=1 & - \\ \hline & & 2a = 1 & \\ &&a=\frac12 \end{array} $$
    • Substitusi $ a = \frac12 $ ke pers(iv) $$\begin{align*} && 108a+6b = 6 \\ &\Leftrightarrow & 108\left(\frac12\right)+6b = 6 \\ &\Leftrightarrow & 54 +6b = 6 \\ &\Leftrightarrow & 6b = -48 \\ &\Leftrightarrow & b = -8 \end{align*}$$
    • Substitusi $ a = \frac12 $ dan $b=-8$ ke pers(i) $$\begin{align*} && 36a+6b+c = 5 \\ &\Leftrightarrow & 36\left(\frac12\right)+6(-8)+c = 5 \\ &\Leftrightarrow & 18 - 48 +c = 5 \\ &\Leftrightarrow & -30 + c = 5 \\ &\Leftrightarrow & c = 35 \end{align*}$$

    Diperoleh nilainya : $ a = \frac{1}{2}, b = -8, $ dan $ c = 35 $

  • Fungsi kuadratnya menjadi $$\begin{align*} y &= ax^2 + bx + c \\ \rightarrow y &= \frac{1}{2}x^2 -8x + 36 \end{align*}$$ Jadi fungsi kuadratnya adalah $ f(x)=y = \frac{1}{2}x^2 -8x + 36$ 😄

Latihan Soal

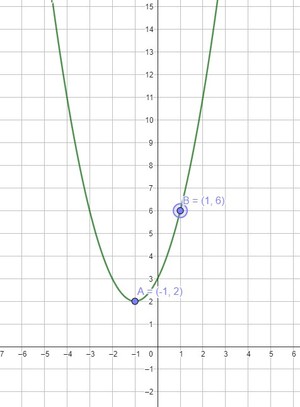
  1. Tentukan fungsi kuadrat yang memiliki titik puncak $(-1,2)$ dan melalui titik $(1,6)$ ? Soal 1

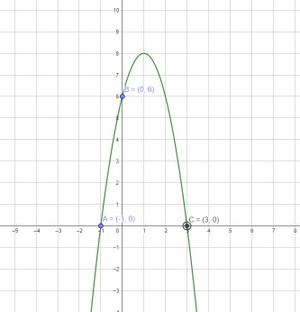
  2. Tentukan fungsi kuadratyang memotong sumbu X di (-1,0) dan (3,0) dan melalui titik (0,6) seperti grafik di bawah ini ? Soal 2

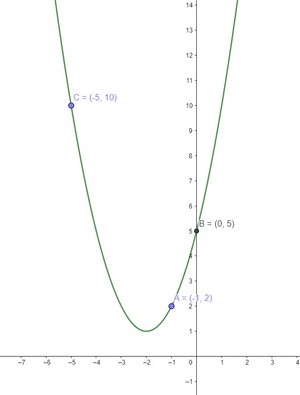
  3. Tentukan fungsi kuadrat yang melalui titik (-5,10), (-1,2), dan (0,5) dari grafik di bawah ini ? Soal 3

Dari ketiga rumus atau cara “Menyusun dan Menentukan Fungsi Kuadrat” ini, cara ketiga yang agak lebih rumit karena kita harus melakukan eliminasi dan substitusi untuk menentukan nilai $ a, b, $ dan $ c $ yang melibatkan tiga variabel. Butuh ketekunan dan ketelitian dalam pengerjaannya, karena salah satu saja maka yang lainnya juga ikut salah.