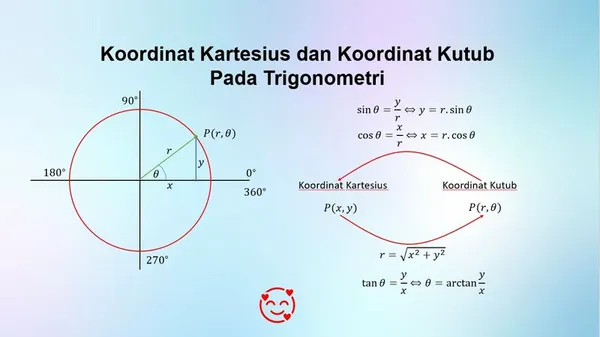
merubah Koordinat Kartesius Menjadi Koordinat Kutub atau Polar dan Sebaliknya pada trigonometri
Kali ini kita akan membahas bagaimana meruah atau mengkonversi koordinat kartesius ke koordinat kutub atau sebaliknya yaitu dari koordinat kutub ke koordinat kartesius. Koordinat suatu titik dapat disajikan dalam bentuk koordinat kutub dan koordinat cartesius. Koordinat kutub sangat berguna salah satunya dalam ilmu navigasi. Koordinat kutub juga sering disebut koordinat polar. Sebelum lanjut pelajari relasi sudut pada trigonometri dan juga nilai trigonometri di berbagai kuadran ya..
Pengertian Koordinat Kartesius
Secara singkat koordinat kartesius adalah suatu titik yang digambar pada sumbu x dan sumbu y, terdiri dari absis (nilai x) dan ordinat (nilai y), ditulis $P(x,y)$. Istilah cartesius sendiri ditemukan oleh ahli matematika dari Perancis yang bernama Rene Descartes. Hasil penemuannya inilah gabungan antara aljabar dan geometri yang kemudian berkembang menjadi ilmu geometri analitik, kalkulus, dan kartografi.
Sistem koordinat cartesius juga bisa digunakan pada dimensi lebih tinggi, misalnya 3 dimensi yang menggunakan sumbu x, y, dan z. Jika pada 2 dimensi digunakan sumbu x dan y, maka sumbu z terletak saling tegak lurus dengan sumbu x dan y.
Manfaat dari koordinat cartesius sendiri banyak digunakan untuk kehidupan sehari-hari. Biasanya koordinat cartesius digunakan pada gambar denah atau peta, sehingga dapat memudahkan dalam mencari sebuah daerah. Selain itu koordinat cartesius juga digunakan dalam bidang penerbangan agar pesawat tidak saling bertabrakan dengan pesawat yang lain.
Pengertian koordinat polar (kutub)
Koordinat kutub atau koordinat polar merupakan sistem koordinat 2 dimensi, dimana titik bidang ditentukan dari jarak titik yang sudah ditetapkan dan besar sudut ditentukan dari arah yang sudah ditetapkan.
Dari abad ke-8 M, penggunaan koordinat kutub ini dikembangkan untuk menghitung arah dan jarak kiblat dari seluruh penjuru bumi.
Koordinat kutub adalah koordinat yang digambar pada sumbu x dan y, terdiri dari nilai r ($r = \sqrt{x^{2}+y^{2}} $) dan sudut θ, yaitu sudut yang dibentuk oleh garis OP dan OX , ditulis $P(r, θ)$. Perhatikan hubungan koordinat kutub dan koordinat kartesius berikut.
Hubungan Koordinat Kartesius dan Koordinat Kutub
Hubungan koodinat kartesius dengan koordinat kutub diperlihatkan oleh gambar berikut ini.
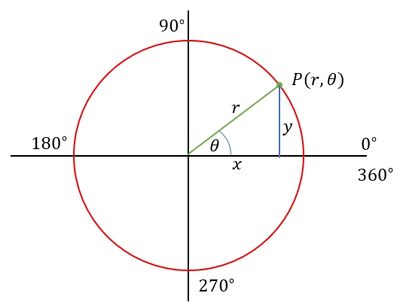
Konversi dari Koordinat Kartesius ke Koordinat Kutub
Dari gambar di atas diperoleh hubungan jika pada koordinat kartesius titik $P (x,y)$ diketahui maka koordinat kutub $P (r,θ)$ dapat ditentukan dengan langkah dan menggunakan rumus sebagai berikut.
- Menentukan nilai $r$
$$r=\sqrt{x^2+y^2}$$ - Menentukan sudut $\theta$
$$\tan \theta=\frac{y}{x}$$ atau $$\theta=\arctan \frac{y}{x}$$ tan berapa yang nilainya y per x. perhatikan juga letak kuadrannya
Konversi dari Koordinat Kutub ke Koordinat Kartesius
Perhatikan gambar diatas lagi ya.. Jika koordinat kutub titik $P (r, θ)$diketahui maka koordinat kartesius titik $P (x, y)$ dapat ditentukan dengan menggunakan langkah dan rumus sebagai berikut.
- Menentukan nilai $x$ $$\cos\theta =\frac{x}{r}\Leftrightarrow x= r\cdot \cos\theta$$
- Menentukan nilai $y$ $$\sin\theta =\frac{x}{r}\Leftrightarrow x= r\cdot \sin\theta$$
Contoh Soal
Nyatakan titik-titik berikut ini kedalam koordinat kutub.
- $P(4,4)$
- $Q(-3,3\sqrt3)$
Alternatif Penyelesaian ✍️
titik $P( 4, 4 )$
artinya $ x = 4$ dan $ y = 4 $- Menentukan jari-jari ($r$) :
$$\begin{align*} r &= \sqrt{x^2 + y^2 } \\&= \sqrt{4^2 + 4^2 } \\&= \sqrt{16 + 16 } \\&= \sqrt{32}=\sqrt{16}\sqrt{2} \\&= 4\sqrt{2} \end{align*}$$ - Menentukan sudut dengan rumus : $ \tan \theta = \dfrac{y}{x} $
$$\begin{align*} \tan\theta &= \frac{y}{x} \\ \tan\theta&= \frac{4}{4} \\ \tan\theta&= 1 \text{ (tan berapa yang nilainya 1)}\\\theta&= \arctan 1 \\ \theta&= 45^\circ \end{align*}$$
Karena nilai $ x $ positif dan $ y $ positif, maka titik P ada di kuadran I dengan sudut $ 45^\circ $
Jadi, koordinat kutubnya adalah $ P (4\sqrt{2}, 45^\circ) $ .- Menentukan jari-jari ($r$) :
titik $Q( -3,3\sqrt3)$
artinya $ x = -3$ dan $ y = 3\sqrt3 $- Menentukan jari-jari ($r$) :
$$\begin{align*} r &= \sqrt{x^2 + y^2 } \\&= \sqrt{(-3)^2 + (3\sqrt3)^2 } \\&= \sqrt{9 + 27 } \\&= \sqrt{36} \\&= 6 \end{align*}$$ - Menentukan sudut dengan rumus : $ \tan \theta = \dfrac{y}{x} $
$$\begin{align*} \tan\theta &= \frac{y}{x} \\ \tan\theta&= \frac{3\sqrt{3}}{-3} \\ \tan\theta&= -\sqrt{3} \text{ (abaikan dulu tanda -)}\\\theta&= \arctan \sqrt{3} \\ \theta&= 60^\circ \end{align*}$$
Karena nilai $ x $ negatif dan $ y $ positif, maka titik Q ada di kuadran II sehingga sudutnya $180^\circ - 60^\circ =120^\circ$
Jadi, koordinat kutubnya adalah $ P (6, 120^\circ) $ .- Menentukan jari-jari ($r$) :
Nyatakan titik-titik berikut ini kedalam koordinat kartesius.
- $P(4,45^\circ)$
- $Q(10,120^\circ)$
Alternatif Penyelesaian ✍️
titik $P(4,45^\circ)$
artinya $ r = 4$ dan $ \theta = 45^\circ $- Menentukan nilai $x$ :
$$\begin{align*} x &= r\cos\theta \\&= 4\cdot\cos 45^\circ \\&= 4\cdot \frac{1}{2}\sqrt{2} \\&= 2\sqrt{2} \end{align*}$$ - Menentukan nilai $y$
$$\begin{align*} y &= r\sin\theta \\&= 4\cdot\sin 45^\circ \\&= 4\cdot \frac{1}{2}\sqrt{2} \\&= 2\sqrt{2} \end{align*}$$
Jadi, koordinat kartesiusnyanya adalah $ P (4\sqrt{2}, 4\sqrt{2}) $ .
- Menentukan nilai $x$ :
titik $Q(10,120^\circ)$
artinya $ r = 10$ dan $ \theta = 120^\circ $- Menentukan nilai $x$ :
$$\begin{align*} x &= r\cos\theta \\&= 10\cdot\cos 120^\circ\\&= 10\cdot\cos (180^\circ-60^\circ)\\&= 10\cdot(-\cos 60^\circ) \\&= 10\cdot (-\frac{1}{2}) \\&= -5 \end{align*}$$ - Menentukan nilai $y$
$$\begin{align*} y &= r\sin\theta \\&= 10\cdot\sin 120^\circ\\&= 10\cdot\sin (180^\circ-60^\circ)\\&= 10\cdot(\sin 60^\circ) \\&= 10\cdot (\frac{1}{2}\sqrt{3}) \\&= 5\sqrt{3} \end{align*}$$
Jadi, koordinat kartesiusnyanya adalah $ P (-5, 5\sqrt{3}) $ .
- Menentukan nilai $x$ :