Menentukan Nilai Perbandingan Trigonometri Sinus, Cosinus, Tangen Di Kuadran I, Kuadran II, Kuadran III, kuadran IV

Kali ini kita akan membahas tentang erbandingan Trigonometri Di Berbagai Kuadran. Sebelumnya Kita telah belajar tentang menentukan nilai perbandingan trigonometri dari sudut lancip pada segitiga siku-siku. Baca Perbandingan Trigonometri pada Segitiga Siku-Siku↝ dan Perbandingan Trigonometri Sudut Istimewa↝ . Konsep ini dapat diperluas untuk berbagai besar sudut. Tentunya nilai dan tanda pada setiap sudut ini berbeda. ada yang positif dan ada yang negatif.

Pada jenjang SMP kita sudah mengenal tentang koordinat kartesius. Sumbu – sumbu pada koordinat membagi bidang koordinat menjadi empat daerah yang disebut sebagai kuadran. Berdasarkan itu maka sudut dalam sebuah koordinat Cartesius dapat dibagi menjadi 4 daerah yang terbagi atas kuadran I, kuadran II, kuadran III, dan kuadran IV. Nah selanjutnya mari kita bahas nilai perbandingan trigonometri di berbagai kuadran.

Nilai Perbandingan Trigonometri di Berbagai Kuadran

Kita ketahui bahwa dalam satu putaran besar sudutnya adalah $360^\circ$. Sebagai sudut putar, sudut dikelompokkan menjadi empat wilayah atau kuadran didasarkan pada besarnya sudut, yaitu:

  1. Kuadran I : dengan sudut $ 0^\circ $ sampai $ 90^\circ $ atau $ 0 < x < \frac{\pi}{2} $
  2. Kuadran II : dengan sudut $ 90^\circ $ sampai $ 180^\circ $ atau $ \frac{\pi}{2} < x < \pi $
  3. Kuadran III : dengan sudut $ 180^\circ $ sampai $ 270^\circ $ atau $ \pi < x < \frac{3\pi}{2} $
  4. Kuadran IV : dengan sudut $ 270^\circ $ sampai $ 360^\circ $ atau $ \frac{3\pi}{2} < x < 2\pi $

dengan nilai $ \pi = 180^\circ $ untuk sudut. Selain sudut pada berbagai kuadran, terdapat pula sudut yang besarnya lebih besar dari $360^\circ$ dan juga sudut negatif.

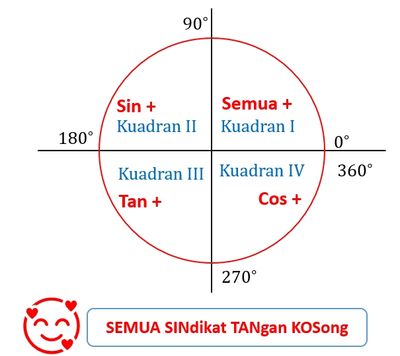
Nilai perbandingan trigonometrinya seperti gambar berikut ini. Nilai Perbandingan Trigonometri di Berbagai Kuadran

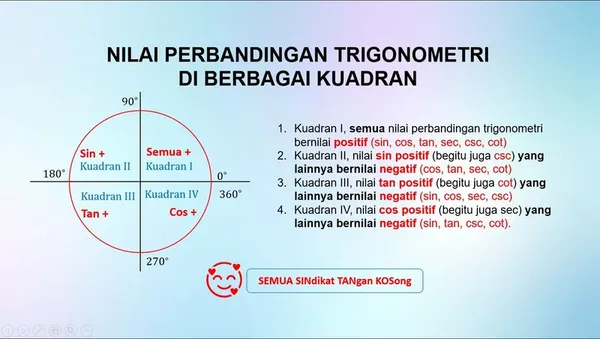
Dari gambar di atas diperoleh,

  1. Kuadran I, semua nilai perbandingan trigonometri bernilai positif (sin, cos, tan, sec, csc, cot)
  2. Kuadran II, nilai sin positif (begitu juga csc) yang lainnya bernilai negatif (cos, tan, sec, cot)
  3. Kuadran III, nilai tan positif (begitu juga cot) yang lainnya bernilai negatif (sin, cos, sec, csc)
  4. Kuadran IV, nilai cos positif (begitu juga sec) yang lainnya bernilai negatif (sin, tan, csc, cot).

Untuk memudahkan mengingat, gunakan kata “SEMUA SINdikat TANgan KOSong”.

Contoh Soal

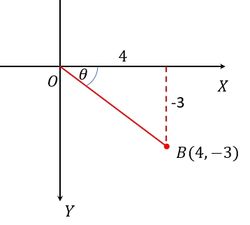
  1. Diketahui titik B(4,-3) jika $\angle XOB=\theta$ tentukan nilai dari $\sin \theta, \cos\theta, \tan\theta$ !

    Alternatif Penyelesaian ✍️

    dengan menggambar titik B pada koordinat cartesius, jelas bahwa titik B berada pada kuadran IV. Nilai Trigonometri Kuadran IV

    Dari gambar diperoleh XB atau panjang sisi depan adalah $y=3$, dan OX atau panjang sisi samping adalah $x=4$. Selanjutnya kita cari panjang OB atau sisi miring dengan menggunakan pythagoras. $$\begin{align*} OB&=\sqrt{x^2+y^2}\\ &=\sqrt{4^2+3^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ OB&=5 \end{align*}$$ Diperoleh panjang sisi miring atau OB=5.

    • Menentukan nilai perbandingan trigonometri $$\begin{align*}\sin \theta & = \frac{de}{mi} = \frac{-3}{5}=-\frac{3}{5} \\\cos \theta & = \frac{sa}{mi} = \frac{4}{5} \\\tan \theta & = \frac{de}{sa} = \frac{-3}{4} = - \frac{3}{4} \end{align*}$$

    Catatan: di kuadran IV, cos bernilai (+), sedangkan sin dan tan bernilai (-)

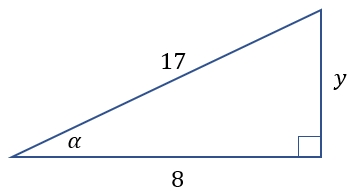
  2. Diketahui nilai $ \cos \alpha = -\dfrac{8}{17} $ dengan $ \alpha $ di kuadran II. Tentukan nilai $ \sin \alpha , $ dan nilai $ \tan \alpha $?

    Alternatif Penyelesaian ✍️

    • Gambar segitiga siku-siku untuk memudahkan.
      nilai $ \cos \alpha = -\dfrac{8}{17} \rightarrow \dfrac{sa}{mi} = \dfrac{-8}{17}, $ artinya sisi samping 8 (abaikan sementara tanda -) dan sisi miring 17, sehingga cari dulu sisi depan dengan teorema pythagoras. misalkan sisi depan $y$ maka $$y=\sqrt{17^2-8^2}=\sqrt{289-64}=\sqrt{225}=15$$ diperoleh sisi depan 15. Nilai Trigonometri Kuadran II
    • Karena $ \alpha $ di kuadran II, maka nilai sin positif dan tan negatif. $$ \begin{align*} \sin \alpha &= \frac{de}{mi} = \frac{15}{17} \\ \tan \alpha &= \frac{de}{sa} = - \frac{15}{8} \end{align*} $$

    Jadi, diperoleh $ \sin \alpha = \frac{15}{17} , $ dan $ \tan \alpha = - \frac{15}{8} $.