Operasi Vektor dalam Matematika

Daftar Isi

1. Penjumlahan Dua Vektor

Jumlah dua vektor atau lebih disebut vektor hasil atau resultan. Secara geometris penjumlahan dua vektor ada 2 aturan, yaitu:

  1. Aturan segitiga Aturan Segitiga
  2. Aturan jajar genjang Aturan Jajargenjang

Pada penjumlahan Vektor berlaku:

  1. Sifat komutatif
    $ \overline{a}+\overline{b}=\overline{b}+\overline{a} $
  2. Sifat asosiatif
    $ \left( \overline{a}+\overline{b} \right)+\overline{c}=\overline{a}+\left( \overline{b}+\overline{c} \right) $
  3. Elemen identitas, yaitu Vektor nol
    $ \overline{a}+\overline{0}=\overline{a}=\overline{0}+\overline{a} $
  4. Invers tambah
    $ \overline{a}+(-\overline{a})=\overline{0} $

2. Resultan dari beberapa vektor

Mengingat aturan segitiga dan sifat asosiatif penjumlahan vektor, maka kita dapat melakukan penjumlahan Vektor dengan cara polygon. Resultan Vektor

3. Selisih Dua Vektor

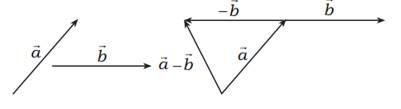
Selisih dua vektor artinya menjumlahkan vektor pertama dengan lawan (negatif) vektor kedua. $$ \overline{a}-\overline{b}=\overline{a}+(-\overline{b})$$ $ \overline{a} $ dikurangi $ \overline{b} $ sama dengan $ \overline{a} $ ditambah lawan dari $ \overline{b} $ . Hal ini diperjelas secara geometri sebagai berikut Selisih Dua Vektor

4. Perkalian Vektor dengan Scalar

Hasil kali vektor $ \overline{a} $ dengan skalar k adalah vektor yang panjangnya k kali panjang vektor $ \overline{a} $ dan arahnya bergantung dengan nilai k. Perkalian Vektor Pada gambar diatas $ \overrightarrow{AB}=\overline{a},\text{ }\overrightarrow{CD}=2\overline{a},\text{ }\overrightarrow{QP}=-\overline{a}, $ dan $ \overrightarrow{KR}=-3\overline{a} $ maka $ \overrightarrow{CD}=2\overrightarrow{AB} $ dan $ \overrightarrow{KR}=3\overrightarrow{QP} $ atau $ \overrightarrow{KR}=-3\overrightarrow{AB} $ .
Dari sini dapat dimengerti bahwa ada 3 kemungkinan hasil kali suatu vektor dengan skalar k yaitu

  1. Jika $ k>0 $ maka $ k.\overline{a} $ adalah suatu vektor yang panjangnya $ k $ kali Vektor $ \overline{a} $ dan searah dengan $ \overline{a} $
  2. Jika $ k=0 $ maka $ k.\overline{a} $ adalah Vektor nol
  3. Jika $ k<0 $ maka $ k.\overline{a} $ adalah suatu vektor yang panjangnya $ k $ kali Vektor $ \overline{a} $ dan berlawanan arah dengan $ \overline{a} $

Jika $ \overline{a} $ suatu Vektor tak nol dan $ n,p\in R $ maka berlaku:

  1. $ n\overline{a}=\left| n \right|.\left| \overline{a} \right| $
  2. $ n(-\overline{a})=-n\overline{a} $
  3. $ n\overline{a}=\overline{a}n $
  4. $ (np)\overline{a}=n(p\overline{a}) $
  5. $ (n+p)\overline{a}=n\overline{a}+p\overline{a} $
  6. $ n(\overline{a}+\overline{b})=n\overline{a}+n\overline{b} $

5. Vektor Posisi

Vektor posisi dari titik A terhadap titik pusat O ditulis $ \overrightarrow{OA} $ atau $ \overline{a} $ . Gambar menunjukkan posisi dari titik A, B, dan C terhadap pusat O, ditulis $ \overrightarrow{OA},\overrightarrow{OB}, $ dan $ \overrightarrow{OC} $ . Vektor $ \overrightarrow{OA},\overrightarrow{OB}, $ dan $ \overrightarrow{OC} $ disebut vektor posisi dari titik A, B, dan C. Vektor posisi dari titik A, B, dan C sering ditulis dengan huruf kecil $ \overline{a},\overline{b}, $ dan $ \overline{c} $ . Vektor Posisi Perhatikan ∆ABO, terlihat bahwa $$ \begin{align*} \overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB} \\ \overrightarrow{AB}=-\overrightarrow{OA}+\overrightarrow{OB} \\ \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA} \end{align*}$$ $ \therefore \overrightarrow{AB}=\overline{b}-\overline{a} $

Contoh

Contoh Menggambar vektor

Diketahui vektor $ \overline{a},\overline{b}, $ dan $ \overline{c} $ digambarkan sebagai berikut Menggambar Vektor Gambarlah diagram vektor diatas yang menunjukkan $ 2\overline{a}+\frac{1}{2}\overline{b}-\frac{2}{3}\overline{c} $ Alternatif penyelesaian Menggambar Vektor Jawaban

Contoh Pembuktian vektor dengan aturan penjumlahan

Buktikan dengan aturan penjumlahan bahwa $ \overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD} $

Alternatif Penyelesaian
$$ \begin{align*} (\overrightarrow{AD}+\overrightarrow{BC})-(\overrightarrow{AC}+\overrightarrow{BD})=\overrightarrow{O}\\ \overrightarrow{AD}+\overrightarrow{BC}-\overrightarrow{AC}-\overrightarrow{BD}=\overrightarrow{O}\\ (\overrightarrow{AD}-\overrightarrow{AC})+(\overrightarrow{BC}-\overrightarrow{BD})=\overrightarrow{O}\\ (\overrightarrow{CA}+\overrightarrow{AD})+(\overrightarrow{DB}-\overrightarrow{BC})=\overrightarrow{O}\\ \overrightarrow{CD}+\overrightarrow{DC}=\overrightarrow{O}\\ \overrightarrow{CC}=\overrightarrow{O} \end{align*}$$ Jadi, $ \overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD} $ (Terbukti)

Contoh Pembuktian Secara Geometri

Pada trapesium ABCD, diberikan titik-titik tengah pada sisi AB, BC, CD, dan DA, yaitu titik P, Q, R, dan S, seperti pada gambar. Buktikan bahwa PQRS merupakan jajargenjang.

Alternatif penyelesaian
Pandang diagonal AC
$$ \begin{align*} \overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BQ} \\ \overrightarrow{PQ}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC} \\ \overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{BC}) \\ \overrightarrow{PQ}=\frac{1}{2}\overrightarrow{AC} \end{align*}$$ $$ \begin{align*} \overrightarrow{SR}=\overrightarrow{SD}+\overrightarrow{DR} \\ \overrightarrow{PQ}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC} \\ \overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{DC}) \\ \overrightarrow{SR}=\frac{1}{2}\overrightarrow{AC} \end{align*}$$ Hal ini berarti $\overrightarrow{PQ}=\overrightarrow{SR}$ dan $\overrightarrow{PQ}$ sejajar $\overrightarrow{SR}$
Jadi, PQRS merupakan jajargenjang.

Contoh Pembuktian vektor secara geometri

Buktikan bahwa diagonal jajargenjang OABC saling berpotongan di tengah

Aternatif penyelesaian
Perhatikan jajargenjang OABC disamping.
Pembuktian vektor secara geometri Vektor posisi dari titik A, B, dan C adalah $ \overline{a},\overline{b}, $ dan $ \overline{c} $ .
M titik tengah $ \overrightarrow{AC} $ , sehingga $$ \begin{align*} \overrightarrow{OM}&=\overrightarrow{OA}+\overrightarrow{AM} \\ \overrightarrow{OM}&=\overrightarrow{OA}+\frac{1}{2}\overrightarrow{AC} \\ \overrightarrow{OM}&=\overrightarrow{OA}+\frac{1}{2}(\overrightarrow{OC}-\overrightarrow{OA}) \\ \overrightarrow{OM}&=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OC}) \\ \overrightarrow{OM}&=\frac{1}{2}(\overline{a}+\overline{c}) \end{align*}$$ Titik tengah $ \overrightarrow{OB} $ ditentukan oleh $ \frac{1}{2}\overline{b} $ , maka $$ \begin{align*} \frac{1}{2}\overline{b}&=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{AB}) \\ \frac{1}{2}\overline{b}&=\frac{1}{2}(\overline{a}+\overrightarrow{OC}) \\ \frac{1}{2}\overline{b}&=\frac{1}{2}(\overline{a}+\overrightarrow{OC}) \\ \frac{1}{2}\overline{b}&=\frac{1}{2}(\overline{a}+\overline{c}) \end{align*}$$ Jadi, titik tengah $ \overrightarrow{AC} $ ditentukan oleh $ \frac{1}{2}(\overline{a}+\overline{c}) $ dan titik titik tengah $ \overrightarrow{OB} $ ditentukan oleh $ \frac{1}{2}\overline{b}=\frac{1}{2}(\overline{a}+\overline{c}) $ . Hal ini menunjukkan bahwa diagonal $ \overrightarrow{OB} $ dan $ \overrightarrow{AC} $ saling berpotongan di tengah

Latihan Soal

  1. Gambarlah vektor-vektor berikut

    • $ \overline{v}=\overline{a}+\overline{b}-\overline{c} $
    • $ \overline{w}=-\frac{2}{3}\overline{a}+\overline{b}-3\overline{c} $

  2. Diketahui ABCDE merupakan segilima beraturan
    Sederhanakanlah

    • $ \overrightarrow{AE}+\overrightarrow{EC}+\overrightarrow{CD}-\overrightarrow{AB} $
    • $ \overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{EC}-\overrightarrow{DE} $

  3. Jika titik A, B, dan M mempunyai vektor posisi $ \overline{a},\overline{b} $ dan $ \overline{m} $ terhadap titik O dan titik M merupakan titik tengah ruas garis AB, buktikan bahwa $ \overline{m}=\frac{1}{2}(\overline{a}+\overline{b}) $

  4. Pada gambar berikut, terlihat bahwa PQRS sebuah jajargenjang. A dan B merupakan titik tengah PQ dan PS Jika $ \overrightarrow{RA}=\overline{u} $ dan $ \overrightarrow{RB}=\overline{v} $ , nyatakan:

    • $ \overrightarrow{PQ} $ dan $ \overrightarrow{RS} $ dalam bentuk $ \overline{u} $ dan $ \overline{v} $
    • $ \overrightarrow{PQ} $ dan $ \overrightarrow{RS} $ dalam bentuk $ \overline{u} $ dan $ \overline{v} $

  5. Pada ∆ABC, $ \overrightarrow{AB},\overrightarrow{BC} $ dan $ \overrightarrow{CA} $ mewakili Vektor-vektor $ \overline{a},\overline{b}, $ dan $ \overline{c} $ . P dan Q adalah titik tengah BC dan CA. Misalkan garis yang melalui Q sejajar BC dan memotong AB di R.

    • Buktikan bahwa $ \overrightarrow{QR} $ mewakili Vektor $ \frac{1}{2}\overline{c}+k\overline{a} $ untuk suatu $ k $
    • Buktikan bahwa $ \overrightarrow{QR} $ mewakili Vektor $ p\overline{b} $ untuk suatu $ p $
    • Dengan menggunakan $ \overline{a}+\overline{b}+\overline{c}=\overrightarrow{O}; $ buktikan bahwa jika $ (l+k)\overline{a}+\left( l+\frac{1}{2} \right)\overline{c}=\overrightarrow{O}, $ maka $ k=\frac{1}{2} $ dan $ l=-\frac{1}{2} $