Penyajian Data dalam Statistika diantaranya Tabel, diagram batang, diagram garis, diagram lingkaran, diagram batang daun, dan diagram kotak garis
Daftar Isi
Penyajian Data merupakan salah satu materi bagian dari Statistika. Untuk penyajian data, data kita bagi menjadi dua bagian yaitu data tunggal dan data berkelompok. Untuk pengertian data tunggal dan data berkelompok, baca materi “statistika secara umum↝ ”.
Penyajian Data Tunggal
Data tunggal dapat disajikan dalam bentuk : Tabel, diagram batang, diagram garis, diagram lingkaran, diagram batang daun, dan diagram kotak garis.
Berikut penjelasan masing-masing penyajian data tunggal.
1. Tabel
Penyajian data tunggal dalam bentuk tabel dinamakan tabel distribusi frekuensi tunggal. Di sini langsung melibatkan frekuensinya masing-masing.
Contoh :
Berikut adalah data ulangan harian matematika dari 40 siswa kelas XII.
83 63 80 73 73 73 87 63
63 73 73 63 73 73 80 83
80 73 63 73 87 67 80 73
73 63 73 83 63 73 83 90
73 73 87 63 73 80 77 77
Dari kumpulan dita di atas, susunlah dalam bentuk tabel!.
Penyelesaian :
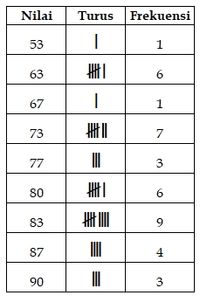
Dari data di atas, terdapat beberapa nilai yang sama. Dapat dibuat dalam Tabel distribusi frekuensi tunggal dengan menghitung masing-masing jumlah yang sama menggunakan tally atau turus. Tally(Turus) menyatakan tanda yang menunjukkan banyakknya data.
2. Diagram Batang
Diagram batang adalah penyajian data dengan menggunakan persegi panjang-persegi panjang dengan arah vertikal atau horizontal. Tinggi setiap persegi panjang batang sesuai dengan jumlah data masing-masing objek. Ada dua jenis diagram batang, yaitu diagram batang vertikal dan diagram batang horizontal.
Contoh :
Jumlah Pengunjung Perpustakaan Umum Kabupaten Kulon Progo menurut Tingkat Pendidikan (Status) Pengunjung pada tahun 2020 adalah sebagai berikut.
| Jenjang | Jumlah |
|---|---|
| PAUD/TK | 3375 |
| SD | 22488 |
| SLTP | 1497 |
| SLTA | 3266 |
| PT | 2525 |
Sumber: BPS
Nyatakan data di atas dalam bentuk diagram batang.
Penyelesaian :
Data tersebut dapat disajikan dengan diagram batang sebagai berikut.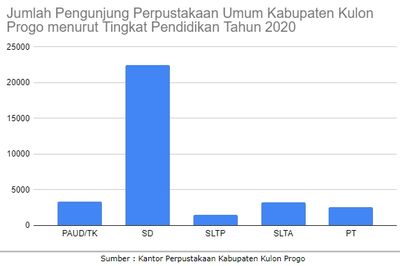
3. Diagram Garis
Diagram garis adalah diagram penyajian data dalam bentuk garis. Diagram garis digunakan untuk menyajikan perkembangan data statistik yang kontinu(berkesinambungan), misalnya jumlah penduduk tiap tahun di suatu wilayah, keadaan suhu badan pasien RS tiap jam, omset penjualan barang di suatu toko. Pada diagram garis, sumbu X (horizontal) biasanya menyatakan satuan waktu, sedangkan sumbu Y (vertikal) biasanya menyatakan frekuensi.
Contoh :
Pada tahun 2022 Indeks harga perdagangan besar bahan bangunan / konstruksi Pekerjaan Umum untuk Jalan, Jembatan dan Pelabuhan seperti tertuang pada tabel berikut.
| Bulan | Indeks harga |
|---|---|
| Januari | 109,88 |
| Februari | 110,19 |
| Maret | 110,94 |
| April | 111,8 |
| Mei | 112,51 |
| Juni | 113,59 |
| Juli | 114,8 |
| Agustus | 116,32 |
| September | 118,59 |
| Oktober | 119,45 |
| November | 119,66 |
Sumber: BPS
Sajikan data diatas ke dalam diagram garis dan kemudian tafsirkan.!
Penyelesaian :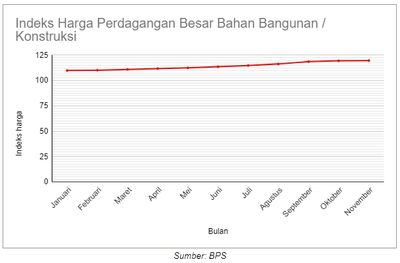
Dari diagram garis di atas dapat dibaca dan ditafsirkan, misalkan :
- Dari diagram diatas terlihat bahwa selama tahun 2022 index harga selalu naik
- Kenaikan yang terbesar terjadi pada bulan September 2022
Grafik Garis Berganda (Multiple Line Chart)
Grafik yang terdiri dari beberapa garis untuk menggambarkan perkembangan beberapa hal atau kejadian sekaligus.
Contoh 2.
Hasil penjualan Barang A dan B di toko “Melati” periode Januari sampai Juni 2019 ditunjukkan pada Tabel di bawah ini.
| Bulan | Jan | Feb | Mar | Apr | Mei | Juni |
|---|---|---|---|---|---|---|
| Jenis Barang A | 25 | 40 | 45 | 10 | 50 | 45 |
| Jenis Barang B | 10 | 15 | 35 | 25 | 40 | 60 |
Data tersebut dapat ditunjukkan dalam diagram garis berganda seperti pada gambar
di bawah ini.
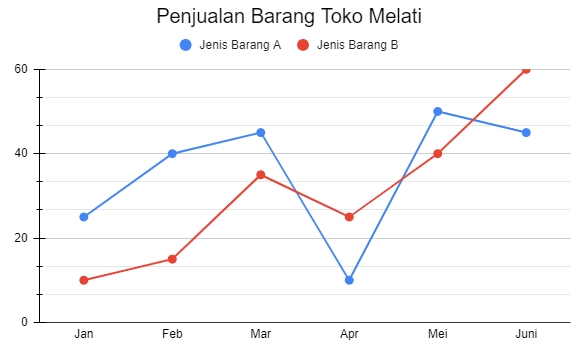
4. Diagram Lingkaran
Diagram lingkaran adalah diagram penyajian data dalam bentuk lingkaran. Bagian-bagian dari daerah lingkaran menunjukkan bagian-bagian atau persen dari keseluruhan. Diagram ini sangat baik untuk menunjukkan perbandingan antara objek yang satu dengan objek lainnya terhadap keseluruhan dalam suatu penyelidikan. Untuk membuat diagram lingkaran, terlebih dahulu ditentukan besarnya persentase tiap objek terhadap keseluruhan data dan besarnya sudut pusat sektor lingkaran.
Cara menentukan besar sudut dan persentase datanya,
- Besar persentase :
Persentase nilai A = - Besar Sudut :
Sudut nilai A =
Untuk memudahkan mengingat, pada lingkaran berlaku perbandingan :
Contoh :
Data berikut ini menunjukkan banyaknya peminat kegiatan ekstra kurikuler siswa kelas XII di SMA Merdeka. Kegiatan Olah raga ada 90 orang, PMR ada 60 orang, dan Paskibra ada 50 orang. Sajikan data di atas dalamt tabel dan diagram lingkaran serta tentukan besar persentasenya masing-masing!
Penyelesaian : Sebelum membuat diagram lingkaran, terlebih dahulu ditentukan besar persentase tiap objek terhadap keseluruhan data dan besar sudut pusat sektor lingkaran yang sesuai sebagaimana ditunjukkan pada tabel di bawah ini.
| Jenis Kegiatan | Jumlah | Persentase | Besar Sudut |
|---|---|---|---|
| PMR | 90 | ||
| Paskibra | 60 | ||
| Olahraga | 50 |
Berikut diagram lingkarannya :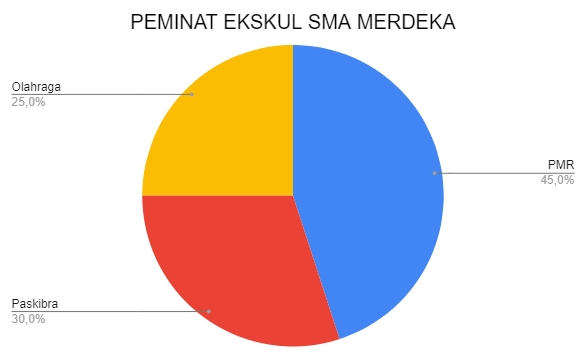
Jenis diagram di atas paling sering kita jumpai dalam kehidupan sehari-hari. Selain penyajian data dengan diagram di atas, juga ada diagram lainnya seperti diagram batang daun (Steam and Leaf Plot), diagram kotak garis, diagram pencar, dan piktogram.
Diagram-diagram di atas umumnya digunakan untuk menyajikan data yang variasi jenis datanya sedikit atau jumlah datanya sedikit. Bagaimana kalau variasi jenis datanya sudah banyak atau data yang diolah dalam jumlah besar? Nah, untuk keperluan penyajian data yang jumlahnya besar, maka pada bagian ini kita akan mempelajari cara menyajikan dalam tabel distribusi frekuensi dan memvisualisasikan ke dalam bentuk grafik histogram, poligon frekuensi, dan ogive.
Penyajian Data Berkelompok
Data tunggal dapat diolah menjadi bentuk-bentuk interval tertentu, data tersebut disebut data berkelompok. Data berkelompok dapat disajikan dalam bentuk tabel distribusi frekuensi berkelompok, histogram, poligon, dan ogif(ogive).
1. Tabel Distribusi Frekuensi berkelompok
Data yang berukuran besar () lebih tepat disajikan dalam tabel distribusi frekuensi berkelompok, yaitu cara penyajian data yang datanya disusun dalam kelas-kelas tertentu.
Langkah-langkah menyusun Tabel Distribusi Frekuensi berkelompok
- Tentukan jangkauannya (J), J = nilai terbesar - nilai terkecil.
- Menentukan banyak interval (K) dengan rumus “Sturgess” yaitu: dengan adalah banyak data.
Banyak kelas harus merupakan bilangan bulat positif hasil pembulatan terbaik. - Menentukan panjang interval kelas (I) dengan menggunakan rumus:
- Menentukan batas-batas kelas. Data terkecil harus merupakan batas bawah interval kelas pertama atau data terbesar adalah batas atas interval kelas terakhir.
- Memasukkan data ke dalam kelas-kelas yang sesuai dan menentukan nilai frekuensi setiap kelas dengan sistem turus atau frekuensi.
Contoh :
Hasil nilai tes matematika 30 siswa kelas XI IPA SMA sebagai berikut :
60 61 30 62 43 55 67 68 69 39
41 63 67 50 76 57 65 49 54 88
40 71 70 51 56 54 78 54 72 69
42 89 70 65 56 58 72 58 73 69
Sajikan data tersebut ke dalam tabel distribusi frekuensi.!
Penyelesaian :
Langkah-langkah menyusun tabel distribusi frekuensi
- Jangkauan (J) =
- Banyak kelas (K)
Banyak kelas dibulatkan menjadi “6”. - Panjang interval kelas (I) adalah .
Panjang interval kelas dibulatkan menjadi “10” (selalu bulatkan ke atas).
Dengan panjang interval kelas = 10 dan banyak kelas = 6, diperoleh tabel distribusi frekuensi berikut.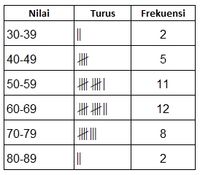
Dari tabel diperoleh beberapa informasi :
Banyak kelas (K) ada enam kelas yaitu 30-39, 40-49, 50-59, 60-69, 70-79, 80-89
Panjang kelas (I) adalah 10 , misalkan: 40-49 memuat nilai 40, 41, 42, 43, dan 49 yaitu mengkover 5 nilai (datum).
Setiap kelas memiliki batas bawah kelas dan batas atas kelas.
Kelas ke-1: 30-39, batas bawahnya 30 dan batas atasnya 39
Kelas ke-2: 40-49, batas bawahnya 40 dan batas atasnya 49
Kelas ke-3: 50-59, batas bawahnya 50 dan batas atasnya 59
Kelas ke-4: 60-69, batas bawahnya 60 dan batas atasnya 69
Kelas ke-5: 70-79, batas bawahnya 70 dan batas atasnya 79
Kelas ke-6: 80-89, batas bawahnya 80 dan batas atasnya 89Setiap kelas memiliki nilai tengah, nilai tengah = (batas bawah + batas atas)
Kelas ke-1: 30-39, nilai tengah
Kelas ke-2: 40-49, nilai tengah
Kelas ke-3: 50-59, nilai tengah
Kelas ke-4: 60-69, nilai tengah
Kelas ke-5: 70-79, nilai tengah
Kelas ke-6: 80-89, nilai tengahSetiap kelas memiliki tepi bawah kelas dan tepi atas kelas.
Tepi bawah = batas bawah - 0,5 .
Tepi atas = batas atas + 0,5 .Kelas ke-1: 30-39, teppi bawahnya 30-0,5=29,5 dan tepi atasnya 39+0,5=39,5
Kelas ke-2: 40-49, teppi bawahnya 40-0,5=39,5 dan tepi atasnya 49+0,5=49,5
Kelas ke-3: 50-59, teppi bawahnya 50-0,5=49,5 dan tepi atasnya 59+0,5=59,5
Kelas ke-4: 60-69, teppi bawahnya 60-0,5=59,5 dan tepi atasnya 69+0,5=69,5
Kelas ke-5: 70-79, teppi bawahnya 70-0,5=69,5 dan tepi atasnya 79+0,5=79,5
Kelas ke-6: 80-89, teppi bawahnya 80-0,5=79,5 dan tepi atasnya 89+0,5=89,5
2. Histogram dan Poligon Frekuensi
Setelah mengelompokkan data ke dalam beberapa kelas menjadi tabel distribusi frekuensi, kita dapat menyajikan data berkelompok tersebut dalam bentuk grafik. Penyajian data dalam bentuk grafik ini bertujuan untuk menyampaikan data kepada pembaca dalam bentuk gambar. Bagi kebanyakan orang, melihat informasi yang disajikan dari gambar lebih mudah daripada melihat dari dari kumpulan bilangan-bilangan pada tabel atau distribusi frekuensi.
Ada tiga macam grafik yang biasanya digunakan untuk menyajikan atau mempresentasikan data berkelompok, yaitu:
- Histogram
- Poligon frekuensi
- Ogive/ grafik frekuensi kumulatif.
Histogram adalah penyajian distribusi frekuensi menggunakan diagram batang tegak. Pada histogram, antara dua batang yang berdampingan tidak terdapat jarak, berbeda dengan penyajian diagram batang terdahulu. Sumbu datar pada histogram menyatakan kelas-kelas interval, sedangkan sumbu tegak menyatakan frekuensi. Dalam hal ini, batas kelas interval merupakan tepi bawah dan tepi atas.
Penyajian histogram dapat disajikan berdasarkan tepi-tepi kelas atau berdasarkan nilai tengah. Jika setiap titik tengah sisi atas persegi panjang yang berdampingan dihubungkan dengan suatu garis, maka terbentuk grafik yang disebut poligon frekuensi.
nilai tengah = (batas bawah + batas atas)
ataunilai tengah = (tepi bawah + tepi atas) .
Tepi bawah kelas ke-
= [ Nilai tengah kelas ke- + Nilai tengah kelas ke- ]Tepi atas kelas ke-
= [ Nilai tengah kelas ke- + Nilai tengah kelas ke- ]Panjang kelas
= Nilai tengah kelas ke- Nilai tengah kelas ke-
Contoh :
Gambarlah histogram dan poligon frekuensi dari tabel distribusi frekuensi berikut ini!
| Nilai Tes Matematika | Frekuensi |
|---|---|
| 30-39 | 2 |
| 40-49 | 4 |
| 50-59 | 8 |
| 60-69 | 10 |
| 70-79 | 5 |
| 80-89 | 1 |
Penyelesaian :
Tabel distribusi
| Nilai Tes Matematika | Frekuensi | Tepi Kelas | Titik Tengah |
|---|---|---|---|
| 30-39 | 2 | 29,5 - 39,5 | 34,5 |
| 40-49 | 4 | 39,5 - 49,5 | 44,5 |
| 50-59 | 8 | 49,5 - 59,5 | 54,5 |
| 60-69 | 10 | 59,5 - 69,5 | 64,5 |
| 70-79 | 5 | 69,5 - 79,5 | 74,5 |
| 80-89 | 1 | 79,5 - 89,5 | 84,5 |
Histogram
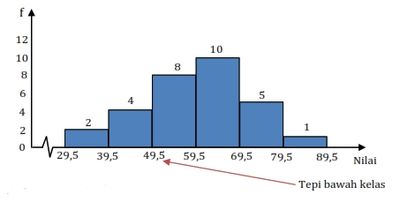
Poligon Frekuensi
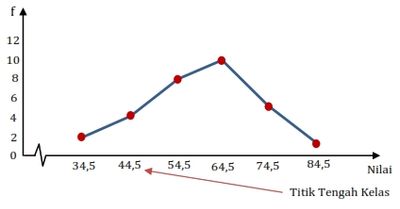
3. Frekuensi Relatif dan Kumulatif
Frekuensi relatif dari suatu data adalah dengan membandingkan frekuensi pada interval kelas itu dengan banyak data dinyatakan dalam persen.
Frekuensi relatif kelas ke- =
Frekuensi kumulatif kelas ke- adalah jumlah frekuensi pada kelas yang dimaksud dengan frekuensi kelas-kelas sebelumnya. Ada dua macam frekuensi kumulatif, yaitu :
- frekuensi kumulatif “kurang dari” (“kurang dari” diambil terhadap tepi atas kelas).
- frekuensi kumulatif “lebih dari” (“lebih dari” diambil terhadap tepi bawah kelas).
contoh :
Dari tabel distribusi frekuensi berikut,
| Nilai Tes Matematika | Frekuensi |
|---|---|
| 30-39 | 2 |
| 40-49 | 4 |
| 50-59 | 8 |
| 60-69 | 10 |
| 70-79 | 5 |
| 80-89 | 1 |
Tentukan :
- Frekuensi relatif untuk interval 50 - 59 (kelas ke-3),
- Tabel Frekuensi kumulatif lebih dari,
- Tabel Frekuensi kumulatif kurang dari.
Penyelesaian :
Frekuensi relatif kelas ke-3= .
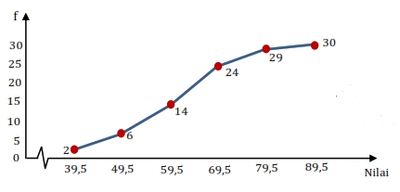
tabel Frekuensi kumulatif kurang dari (menggunakan tepi atas)
Nilai Frekuensi kumulatif 39,5 2 49,5 2 + 4 = 6 59,5 6 + 8 = 14 69,5 14 + 10 = 24 79,5 24 + 5 = 29 89,5 29 + 1 = 30 Tabel Frekuensi kumulatif lebih dari (menggunakan tepi bawah)
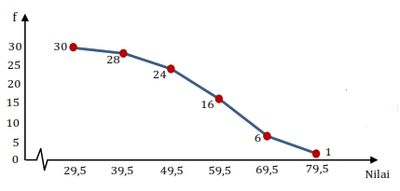
| Nilai | Frekuensi kumulatif |
|---|---|
| 29,5 | 28 + 2 = 30 |
| 39,5 | 24 + 4 = 28 |
| 49,5 | 16 + 8 = 24 |
| 59,5 | 6 + 10 = 16 |
| 69,5 | 1 + 5 = 6 |
| 79,5 | 1 |
Dari tabel distribusi frekuensi kumulatif kurang dari dan lebih dari, kita dapat menggambarkan ogive kurang dari atau ogive positif dan ogive lebih dari atau ogive negatif.
4. Ogif (ogive)
Grafik yang menunjukkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari dinamakan poligon kumulatif. Untuk populasi yang besar, poligon mempunyai banyak ruas garis patah yang menyerupai kurva sehingga poligon frekuensi kumulatif dibuat mulus, yang hasilnya disebut ogif.
Ada dua macam ogif, yaitu sebagai berikut.
- Ogif dari frekuensi kumulatif kurang dari disebut ogif positif.
- Ogif dari frekuensi kumulatif lebih dari disebut ogif negatif.
Contoh :
Hasil tes ulangan Matematika terhadap 30 siswa kelas XII IPA digambarkan dalam tabel di bawah ini.
| Nilai Tes Matematika | Frekuensi |
|---|---|
| 30-39 | 2 |
| 40-49 | 4 |
| 50-59 | 8 |
| 60-69 | 10 |
| 70-79 | 5 |
| 80-89 | 1 |
| 30 |
Gambarkan ogive positif dan ogive negatif dari tabel distribusi frekuensi kumulatif diatas.
Penyelesaian :
- Daftar frekuensi kumulatif kurang dari dan lebih dari
| Nilai Tes Matematika | Frekuensi | Frekuensi kumulatif | Frekuensi kumulatif |
|---|---|---|---|
| 30-39 | 2 | 2 | 30 |
| 40-49 | 4 | 6 | 28 |
| 50-59 | 8 | 14 | 24 |
| 60-69 | 10 | 24 | 16 |
| 70-79 | 5 | 29 | 6 |
| 80-89 | 1 | 30 | 1 |
Ogive positif, diperoleh dari tabel distribusi frekuensi kumulatif kurang dari.

Ogive negatif, diperoleh dari tabel distribusi frekuensi kumulatif lebih dari.

Dari kedua gambar diatas terlihat bahwa ogive positif kurvanya selalu naik, sedangkan ogive negatif kurvanya selalu turun.
Demikian mengenai statistika penyajian data, selanjutnya adalah kita akan belajar tentang statistika ukuran pemusatan data.