menentukan nilai perbandingan trigonometri sudut istimewa 0°, 30°, 45°, 60°, 90° dan penyelesainnya dalam sehari-hari
Trigonometri mengkaji hubungan antara sisi dan sudut dalam suatu segitiga dan sifat-sifat serta aplikasinya dalam berbagai bidang seperti penaksiran tinggi bangunan atau pohon, jarak mendatar puncak gunung terhadap lembahnya, dan sebagainya. Kali ini kita akan membahas tentang perbandingan trigonometri untuk sudut istimewa. Agar lebih mudah memahami ini baca terlebih dahulu Perbandingan Trigonometri pada Segitiga Siku-Siku↝ .
Sudut istimewa adalah suatu sudut di mana nilai perbandingan trigonometrinya dapat ditentukan secara langsung tanpa menggunakan daftar trigonometri atau kalkulator.
Sudut-sudut yang dimaksud adalah sudut-sudut yang besarnya $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ dan $90^\circ$.
Bagaimana cara menentukan nilai perbandingan trigonometri sudut-sudut istimewa tersebut? Berikut penjelasananya…
Nilai Perbandingan Trigonometri Sudut Istimewa Kuadran I
Kita mulai dari segitiga sama sisi ABC dengan panjang sisi 2 satuan. Karena segitiga sama sisi, maka ketiga sisinya sama panjang dan ketiga sudutnya juga sama yaitu 60°.
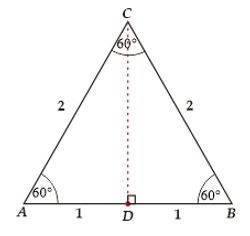Misalkan CD adalah garis tinggi sekaligus garis bagi segitiga ABC maka garis CD dapat kita cari dengan menggunakan teorema pythagoras.
$$\begin{align*}CD&=\sqrt{BC^2-DB^2}\\&=\sqrt{2^2-1^2}\\&=\sqrt{4-1}\\CD&=\sqrt{3}\end{align*}$$
Dengan demikian, Kita dapat menentukan nilai perbandingan trigonometri untuk sudut 30° dan 60°. Perhatikan segitiga BCD dan ingat sindemi cossami tandesa...
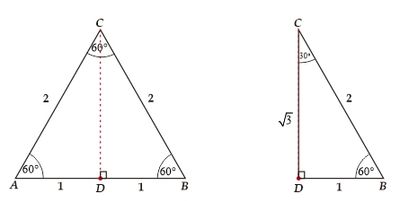
Trigonometri Sudut 30°
Nilai perbandingan trigonometri sudut 30° sebagai berikut: $$\begin{align*}\sin 30^\circ&=\frac{de}{mi}=\frac{BD}{BC}=\frac{1}{2}\\\cos 30^\circ&=\frac{sa}{mi}=\frac{CD}{BC}=\frac{\sqrt3}{2}=\frac{1}{2}\sqrt{3}\\\tan 30^\circ&=\frac{de}{sa}=\frac{BD}{CD}=\frac{1}{\sqrt3}=\frac{1}{3}\sqrt{3}\end{align*}$$
Trigonometri Sudut 60°
Nilai perbandingan trigonometri sudut 60° sebagai berikut: $$\begin{align*}\sin 60^\circ&=\frac{de}{mi}=\frac{BD}{BC}=\frac{1}{2}\\\cos 60^\circ&=\frac{sa}{mi}=\frac{BD}{BC}=\frac{\sqrt3}{2}=\frac{1}{2}\sqrt{3}\\\tan 60^\circ&=\frac{de}{sa}=\frac{BD}{BC}=\frac{1}{\sqrt3}=\frac{1}{3}\sqrt{3}\end{align*}$$
Trigonometri Sudut 45°
Perhatikan segitiga ABC dibawah ini.
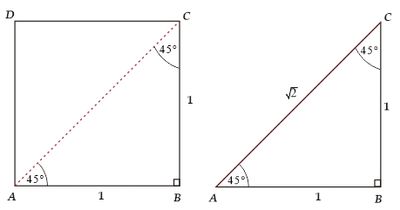
Nilai perbandingan trigonometri sudut 45° sebagai berikut: $$\begin{align*}\sin 45^\circ&=\frac{de}{mi}=\frac{AB}{AC}=\frac{1}{\sqrt2}=\frac12 \sqrt2\\\cos 45^\circ&=\frac{sa}{mi}=\frac{BC}{AC}=\frac{1}{\sqrt2}=\frac12 \sqrt2\\\tan 45^\circ&=\frac{de}{sa}=\frac{AB}{BC}=\frac{1}{1}=1\end{align*}$$
Secara lengkap dan ringkasan dari tulisan diatas, nilai perbandingan trigonometri sudut istimewa di kuadran I adalah sebagai berikut:
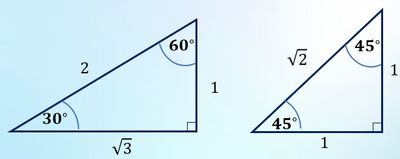
Tabel Nilai Trigonometri
| $\theta$ | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|
| $0^\circ$ | 0 | 1 | 0 |
| $30^\circ$ | $\dfrac{1}{2}$ | $\dfrac{1}{2}\sqrt3$ | $\dfrac{1}{3}\sqrt3$ |
| $45^\circ$ | $\dfrac{1}{2}\sqrt2$ | $\dfrac{1}{2}\sqrt2$ | 1 |
| $60^\circ$ | $\dfrac{1}{2}\sqrt3$ | $\dfrac{1}{2}$ | $\sqrt3$ |
| $90^\circ$ | 1 | 0 | - |
Contoh Soal
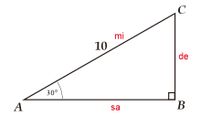
Diketahui segitiga ABC siku-siku di B, jika panjang AC adalah 10 cm, dan $\angle A = 30^\circ$. Hitunglah panjang AB dan BC.
Alternatif Penyelesaian ✍️
Diketahui:
$\triangle ABC$ siku-siku di B
$\angle A=30^\circ$
$AC=10$ cm- Gambar $\triangle ABC$
- cari panjang AB
untuk mencari panjang AB kita dapat membandingkannya menggunakan perbandingan trigonometri. AB merupakan sisi samping sehingga kita bisa menggunakan cosinus
$$\begin{align*} \cos A&=\frac{sa}{mi}\\ \cos 30^\circ&=\frac{AB}{AC}\\ \frac{\sqrt{3}}{2}&=\frac{AB}{10}\\ AB&=\frac{10\times \sqrt3}{2}\\ AB&=5\sqrt3\end{align*}$$ - cari panjang BC gunakan sinus
$$\begin{align*} \sin A&=\frac{de}{mi}\\ \sin 30^\circ&=\frac{BC}{AC}\\ \frac12&=\frac{BC}{10}\\ BC&=\frac{10\times 1}{2}\\ BC&=5\end{align*}$$
Jadi, panjang $AB=5\sqrt3$ cm dan $BC=5$
- Gambar $\triangle ABC$
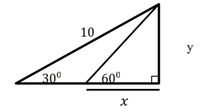
Hitunglah nilai 𝑥 pada gambar berikut ini.
Alternatif Penyelesaian ✍️
untuk menentukan nilai x kita terlebih dahulu menentukan nilai y- menentukan nilai y $$\begin{align*}\sin 30^\circ&=\frac{y}{10}\\ \frac{1}{2}&=\frac{y}{10}\\ y&=\frac{10\times 1}{2}\\ y&=5 \end{align*}$$
- menentukan nilai x $$\begin{align*}\tan 60^\circ&=\frac{y}{x}\\ \frac{\sqrt{3}}{1}&=\frac{5}{x}\\ x&=\frac{5\times 1}{\sqrt{3}}\\ x&=\frac{5}{3}\sqrt{3} \end{align*}$$
Jadi, nilai x adalah $\frac{5}{3}\sqrt{3}$.
Nilai trigonometri dari sebuah sudut dapat dicari dengan menggunakan tabel trigonometri atau dengan menggunakan kalkulator ilmiah (scientific calculator). Yang perlu dicermati, kita harus menentukan dulu satuan sudut yang digunakan. Satuan derajat menggunakan simbol “$\circ$”, sedangkan radian tidak menggunakan satuan ukuran (tanpa dimensi) atau ada juga dengan simbol rad.
Penerapan Trigonometri Dalam Kehidupan Sehari-hari
Banyak sekali penerapan trigonometri dalam kehidupan sehari-hari. Perbandingan trigonometri dapat digunakan untuk memecahkan masalah kontekstual yang berhubungan dengan sudut pengamatan, bidang navigasi, astronomi, teknik sipil, mengukur tinggi suatu benda, atau untuk menentukan jarak ke suatu obyek.
Beberapa keterampilan yang perlu kalian miliki untuk meningkatkan kemampuan memecahkan masalah adalah:
- Memahami soal
Pahami soal atau masalah yang diberikan - Memilih pendekatan atau strategi pemecahan
Setelah memahami soal, pilih rumus/metode utuk penyelesaian - Menyelesaikan model
Setelah memilih strategi penyelesaian, lakukan operasi hitung atau operasi aljabar secara benar untuk mendapatkan solusi dari permasalahan yang diberikan - Menafsirkan solusi
Setelah solusi atau penyelesaian dari model matematika diperoleh, selanjutnya periksalah kelayakan atau kebenaran jawaban atau masuk akalnya jawaban
Untuk lebih memahami perhatikan contoh berikut:
Contoh Soal
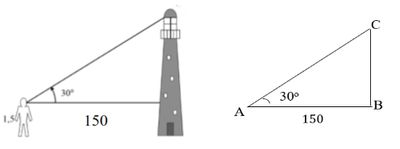
Sebuah Menara berjarak 150 meter dari Andi yang tingginya 150 cm. Apabila puncak menara tersebut dilihat Andi dengan menggunakan klinometer didapat sudut elevasi (sudut yang dibentuk oleh arah horizontal dengan arah pandangan mata pengamat ke arah atas) $30^\circ$, tentukanlah tinggi menara tersebut.
Alternatif Penyelesaian ✍️
memahami masalah Diketahui :
Sudut elevasi = $30^\circ$
Jarak Andi dengan Menara = 150 meter
Jarak mata Andi dengan tanah = 150 cm
Dicari: tinggi pohonSketsa posisi Andi dengan menara:
Memilih pendekatan atau strategi pemecahan
Konsep yang relevan dari soal di atas adalah perbandingan trigonometri. Misalkan AB jarak menara dengan Andi, dan BC tinggi menara dikurangi tinggi Andi. $$\tan A=\frac{de}{sa}=\frac{BC}{AB}$$Menyelesaikan model (mencari panjang BC) $$\begin{align*} \tan A&=\frac{BC}{AB}\\ \tan 30^\circ&=\frac{BC}{150}\\\frac{\sqrt{3}}{3}&=\frac{BC}{150}\\ BC&=\frac{150\times \sqrt{3}}{3}\\ BC&=50\sqrt{3}\end{align*}$$
Menafsirkan solusi
$$\begin{align*}\text{Tinggi menara} &= BC + \text{tinggi Andi}\\ &= 50\sqrt{3} + 1,5 \\ & \approx 86,602 + 1,5 \\ &\approx 88,102\end{align*}$$ Jadi, tinggi menara adalah $(50\sqrt{3} + 1,5)$ m atau sekitar 88,102 m.
Demikian artikel tentang Perbandingan Trigonometri Sudut Istimewa↝ semoga bermanfaat.
Latihan Soal
- Diketahui segitiga $ABC$ siku-siku di $B$, jika panjang $AC$ adalah 8 cm, dan $\angle A = 30^\circ$. Hitunglah panjang $AB$ dan $BC$.
- Seorang anak memandang sebuah pohon dengan sudut $60^\circ$. Apabila jarak anak tersebut 60 meter dari pohon, tentukan tinggi pohon tersebut.
- Andi melihat sebuah sebuah menara dari jarak 150 meter dengan sudut elevasi $30^\circ$. Jarak mata Andi dengan tanah 150 cm. Tentukan tinggi gedung tersebut!