Persamaan trigonometri adalah persamaan yang memuat perbandingan trigonometri (ukuran derajat atau radian). Ketika menyelesaikan sembarang persamaan trigonometri, maka yang harus kita lakukan adalah mengubah persamaan tersebut ke dalam persamaan trigonometri sederhana.

Persamaan trigonometri adalah persamaan yang memuat perbandingan trigonometri (ukuran derajat atau radian). Ketika menyelesaikan sembarang persamaan trigonometri, maka yang harus kita lakukan adalah mengubah persamaan tersebut ke dalam persamaan trigonometri sederhana. Dalam menyelesaikan persamaan trigonometri pastikan kamu telah mempelajari materi prasyaratnya yaitu trigonometri dasar↝

Persamaan trigonometri bentuk $\sin x=\sin \alpha $

Perhatikan grafik sinus berikut

Grafik fungsi sinus

Gambar 4. Grafik fungsi sin x

Grafik sinus berulang-ulang naik turun, seperti huruf “S” tidur terbalik. Berulang-ulangnya setiap 360°. Pada gambar diatas, nilai awal grafik sinus di kuadran I adalah positif. Nilai sinus akan kembali positif di kuadran II. Oleh karena itu,

Persamaan trigonometri bentuk $\cos x=\cos \alpha $

Perhatikan grafik cosinus berikut

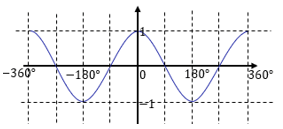Grafik fungsi cosinus Gambar 5. Grafik fungsi cos x

Grafik cosinus berulang-ulang naik turun, seperti huruf “C” tidur. Berulang-ulangnya setiap 360°. Pada gambar diatas, nilai awal grafik cosinus di kuadran I adalah positif. Nilai cosinus akan kembali positif di kuadran IV. Oleh karena itu,

Persamaan trigonometri bentuk $\tan x=\tan \alpha $

Perhatikan grafik cosinus berikut

Grafik fungsi tangen Gambar 6. Grafik fungsi tan x

Grafik tangen berulang-ulang terputus-putus dan berulang-ulangnya setiap 180°. Pada gambar diatas nilai positif berada di kuadran I dan berulang setiap 180°. Oleh karena itu,

Agar lebih mudah dalam memahaminya perhatikan contoh berikut

Contoh

Tentukan penyelesaian dari setiap persamaan trigonometri berikut.

  1. $\sin x=\sin 40^\circ ,\text{ }0\le x\le 360^\circ$
  2. $\cos (2x-\pi )=\cos \frac{\pi }{6},\text{ }0\le x\le 2\pi $
  3. $\tan 3x=\tan x,\text{ }0\le x\le 360^\circ $

Alternatif Penyelesaian

  1. $\sin x=\sin 40^\circ,0\le x\le 360^\circ $

    1. $x_1=40^\circ +k.360^\circ $
      Untuk $k=0\to {{x}_{1}}=40^\circ $
    2. $x_2=(180^\circ -40^\circ )+k.360^\circ $
      Untuk $k=0\to {{x}_{2}}=140^\circ $

    Jadi, Himpunan Penyelesaiannya adalah HP= ${40^\circ ,140^\circ }$

  2. $\cos (2x-\pi )=\cos \frac{\pi }{6},\text{ }0\le x\le 2\pi $

    1. $2x_1-\pi =\frac{\pi }{6}+k.2\pi $
      $x_{1}=\frac{7}{12}\pi +k.\pi$
      Untuk $k=0\to x_1=\frac{7}{12}\pi$
      Untuk $k=1\to x_1=\frac{19}{12}\pi$
    2. $2x_2-\pi =(-\frac{\pi }{6})+k.2\pi $
      $x_2=\frac{5}{12}\pi +k.\pi $
      Untuk $k=0\to x_{2}=\frac{5}{12}\pi$
      Untuk $k=1\to x_2=\frac{17}{12}\pi $

    Jadi, Himpunan Penyelesaiannya adalah HP= ${\frac{5}{12}\pi ,\frac{7}{12}\pi ,\frac{17}{12}\pi ,\frac{19}{12}\pi }$

  3. $\tan 3x=\tan x,\text{ }0\le x\le 360^\circ $
    $3x=x+k.180^\circ$
    $2x=k.180^\circ$
    $x=k.90^\circ$
    Untuk
    $k=0\to x=0$
    $k=1\to x=90^\circ$
    $k=2\to x=180^\circ$
    $k=3\to x=270^\circ$
    $k=4\to x=360^\circ$

    Jadi, Himpunan Penyelesaiannya adalah HP= ${0^\circ ,90^\circ ,180^\circ ,270^\circ ,360^\circ }$