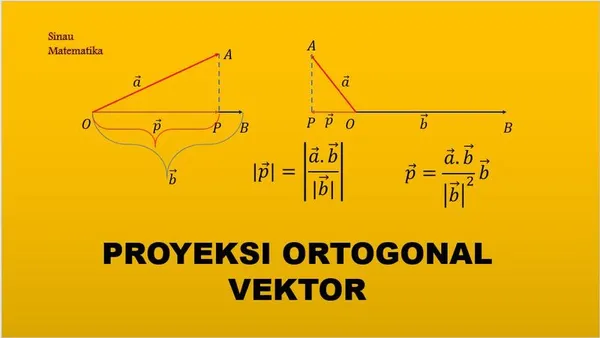
Proyeksi orthogonal suatu vektor ke vektor yang lain, hasilnya berupa vektor. Sedangkan panjang proyeksi vektor orthogonal suatu vektor pada vektor yang lain selalu bernilai bilangan/skalar real positif.
Pada artikel kali ini kita akan membahas proyeksi vektor khususnya proyeksi vektor secara ortogonal (tegak lurus).
Proyeksi orthogonal suatu vektor ke vektor yang lain, hasilnya berupa vektor. Sedangkan panjang proyeksi vektor orthogonal suatu vektor pada vektor yang lain selalu bernilai bilangan/skalar real positif.
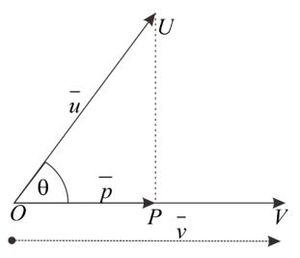Proyeksi orthogonal vektor $\vec{u}$ pada vektor $\vec{v}$ dapat dinotasikan oleh ${\vec{u}}_{\vec{v}}$ atau $\vec{p}$ dan ditentukan oleh dalil berikut.
Dalil :
- Proyeksi skalar orthogonal $\vec{u}$ pada $\vec{v}$ adalah $$\left| \left| \vec{p}\right| \right|=\frac{\vec{u}\cdot\vec{v}}{\left| \vec{v}\right|}$$
- Proyeksi vektor $\vec{u}$ ke vektor $\vec{v}$ adalah vektor $${\vec{u}}_{\vec{v}}=\left( \frac{\vec{u} \cdot \vec{v}}{\left| \vec{v} \right|^2} \right)\vec{v}\text{ atau } \vec{p}=\frac{\vec{u}}{\left| \vec{v} \right|} \left| \left| \vec{p} \right| \right|$$
- Panjang proyeksi vektor $\vec{u}$ ke vektor $\vec{v}$ adalah $$ \lvert \vec{u}_{\vec{v}}\rvert=\left| \vec{u}\cdot e_{\vec{v}} \right| $$ dengan $e_{\vec{v}}$ adalah vektor satuan ke arah $\vec{v}$ atau $\left| \vec{u}_{\vec{v}} \right|=\left| \frac{\vec{u}.\vec{v}}{\left| \vec{v} \right|} \right|$ .
Contoh 1:
Diketahui $\vec{a}=2\widehat{i}-6\widehat{j}-3\widehat{k}$ dan $\vec{b}=4\widehat{i}+2\widehat{j}-4\widehat{k}$. Tentukan:
- Panjang proyeksi vektor $\vec{a}$ pada $\vec{b}$
- Proyeksi orthogonal vektor $\vec{a}$ pada $\vec{b}$
- Proyeksi orthogonal vektor $\vec{b}$ pada $\vec{a}$
Alternatif Penyelesaan:
Panjang proyeksi vektor $\vec{a}$ pada $\vec{b}$ $$\begin{align*} \left| \vec{a}_{\vec{b}} \right|=\left| \frac{\vec{a}.\vec{b}}{\left| \vec{b} \right|} \right|&=\left| \frac{(2\widehat{i}-6\widehat{j}-3\widehat{k})\cdot (4\widehat{i}+2\widehat{j}-4\widehat{k})}{\sqrt{{{4}^{2}}+{{2}^{2}}+{{(-4)}^{2}}}} \right| \\ &=\left| \frac{(2)(4)+(-6)(2)+(-3)(-4)}{\sqrt{16+4+16}} \right| \\ &=\left| \frac{8-12+12}{\sqrt{36}} \right|=\left| \frac{8}{6} \right| \end{align*}$$ $ \therefore \left| \vec{a}_{\vec{b}} \right|=\frac{4}{3}$
Proyeksi orthogonal vektor $\vec{a}$ pada $\vec{b}$
$\vec{a}_{\vec{b}}=\left| \left| \vec{a}_{\vec{b}} \right| \right|\frac{\vec{b}}{\left| \vec{b} \right|}$, karena $\left| \vec{b} \right|=6$ dan $\left| \left| {{\vec{a}}_{\vec{b}}} \right| \right|=\frac{4}{3}$
$$\begin{align*} \vec{a}_{\vec{b}}&=\frac{4}{3}.\frac{4\widehat{i}+2\widehat{j}-4\widehat{k}}{6} \\ & =\frac{8}{9}\widehat{i}+\frac{4}{9}\widehat{j}-\frac{8}{9}\widehat{k} \end{align*}$$Proyeksi orthogonal vektor $\vec{b}$ pada $\vec{a}$
$$\begin{align*}\vec{b}_{\vec{a}}&=\left( \frac{\vec{b}\cdot \vec{a}}{{{\left| \vec{a} \right|}^{2}}} \right)\vec{a} \\ &=\frac{(4\widehat{i}+2\widehat{j}-4\widehat{k})\cdot (2\widehat{i}-6\widehat{j}-3\widehat{k})}{{{\left( \sqrt{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}} \right)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{(4)(2)+(2)(-6)+(-4)(-3)}{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{8}{49}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ \vec{b}_{\vec{a}}&=\frac{16}{49}\widehat{i}-\frac{48}{49}\widehat{j}-\frac{24}{49}\widehat{k})\end{align*}$$
contoh 2
Diketahui vektor-vektor $ \vec{u} = (-1,1,-4) $ dan $ \vec{v} = ( 2, -1,3) $ . Tentukan proyeksi skalar dan proyeksi vektor $ (2\vec{u} + 3\vec{v}) $
pada $ -2\vec{v} $!
Penyelesaian :
misalkan :
$ \vec{a} = (2\vec{u} + 3\vec{v}) = (-2,2,-8) + ( 6, -3,9) = (4, -1 , 1) $
$ \vec{b} = -2 \vec{v} = ( -4, 2,-6) $
- Menentukan proyeksi skalar $ \vec{a} $ pada $ \vec{b} $
$$\begin{align*}\text{Proyeksi skalar } &= \frac{\vec{a}.\vec{b}}{|\vec{b}|} \\&= \frac{4.(-4) + (-1). 2 + 1. (-6)}{\sqrt{(-4)^2 + 2^2 + (-6)^2} } \\&= \frac{-16 - 2 - 6}{\sqrt{16 + 4 + 36 } } \\&= \frac{-24}{\sqrt{56} } \\&= \frac{-24}{56} \sqrt{56} \\&= -\frac{3}{7} \sqrt{56}\end{align*}$$
$\therefore$ sehingga proyeksi skalarnya adalah $ -\frac{3}{7} \sqrt{56} $. - Menentukan proyeksi vektor $ \vec{a} $ pada $ \vec{b} $
$$\begin{align*}\text{Proyeksi vektor } &= \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2} \right) \vec{b}\\&= \left( \frac{-24}{(\sqrt{56})^2} \right) ( -4, 2,-6)\\&= \left( \frac{-24}{56} \right) ( -4, 2,-6)\\ &= \left( -\frac{3}{7} \right) ( -4, 2,-6)\\&= \left( \frac{12}{7}, -\frac{6}{7}, \frac{18}{7} \right)\end{align*}$$
$\therefore$ jadi, proyeksi vektornya adalah $ \left( \frac{12}{7}, -\frac{6}{7}, \frac{18}{7} \right) $.
Contoh 3
Diketahui vektor $ \vec{p} = 2\vec{i}+\vec{j} +2\vec{k} $ dan $ \vec{q} = 3\vec{i} + b\vec{j} + \vec{k} $. Jika $ |\vec{r}| $ adalah panjang proyeksi
vektor $ \vec{q} $ pada $ \vec{p} $ dan $ |\vec{r}| = 4 $, maka tentukan nilai $ b $!
Penyelesaian :
Diketahui vektor $ \vec{p} = (2, 1, 2) $ dan $ \vec{q} = (3, b, 1) $ .
- Menentukan nilai $ b $ dengan proyeksi ortogonal $ \vec{q} $ pada $ \vec{p} $ :
$$\begin{align*}\text{Panjang proyeksi } &= \left| \frac{\vec{q}.\vec{p}}{|\vec{p}|} \right|\\|\vec{r}| &= \left| \frac{\vec{q}.\vec{p}}{|\vec{p}|} \right|\\4 &= \left| \frac{ 2.3 + 1.b + 2.1 }{ \sqrt{2^2 + 1^2 + 2^2 } } \right|\\4 &= \left| \frac{ b + 8 }{ \sqrt{9} } \right|\\4 &= \left| \frac{ b + 8 }{ 3 } \right| \\| b + 8 | &= 12 \\ b &= 4 \vee b = -20 \end{align*}$$
Jadi, nilai $ b $ yang mungkin adalah $ b = -20 $ atau $ b = 4 $.
Contoh 4
Tentukan proyeksi vektor $ \vec{a} = (2,0,1) $ pada vektor $ \vec{b} $ yang sejajar dan sama panjang tetapi berlawanan arah dengan
vektor $ \vec{c} = (0, 2, -2 ) $ !
Penyelesaian :
Diketahui vektor $ \vec{b} = - \vec{c} = -(0, 2, -2) = (0, -2, 2) $.
- Menentukan proyeksi vektor $ \vec{a} $ pada $ \vec{b} $ :
$$\begin{align*}\text{Proyeksi vektor } &= \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2} \right) \vec{b} \\&= \left( \frac{2.0 + 0. (-2) + 1.2}{(\sqrt{0^2 + (-2)^2 + 2^2 })^2 } \right) (0, -2, 2)\\&= \left( \frac{2}{(\sqrt{8 })^2 } \right) (0, -2, 2)\\ &= \left( \frac{2}{8 } \right) (0, -2, 2) \\&= \left( \frac{1}{4 } \right) (0, -2, 2)\\&= \left( 0, -\frac{1}{2} , \frac{1}{2} \right) \end{align*}$$
Jadi, hasil proyeksi vektornya adalah $ \left( 0, -\frac{1}{2} , \frac{1}{2} \right) $.