Rumus Jumlah Dan Selisih Dua Sudut Pada Trigonometri

Kali ini akan di bahas Rumus Jumlah Dan Selisih Dua Sudut pada Trigonometri beserta bukti dan contoh soalnya

Trigonometri adalah materi Matematika yang selalu ada di setiap tingkat kelas jenjang SMA baik kelas X, XI, atau XII. Pada kelas X ada perbandingan, fungsi, dan identitas trigonometri. Di Kelas XI ada Persamaan Trigonometri dan Rumus Jumlah dan Selisih dua sudut. Sedangkan di kelas XII ketemu trigonometri ketika menghitung integral tak tentu dan integral tentu dari fungsi trigonometri.

Kali ini, kita akan sama-sama belajar tentang Rumus Jumlah dan Selisih Sudut Pada Trigonometri. Ini merupakan materi trigonometri lanjutan. Materi ini digunakan untuk menghitung nilai sudut trigonometri yang tidak istimewa. Misalkan $\sin 75^\circ$, dapat kita tuliskan dengan penjumlahan sudut istimewa $\sin 75^\circ=\sin (45^\circ+30^\circ)$. Misalkan lagi $\cos 15^\circ$, dapat kita tuliskan dengan pengurangan atau selisih sudut istimewa $\cos 15^\circ=\cos (45^\circ-30^\circ)$.

Untuk memudahkan pemahaman tentang materi ini, tentu harus paham dulu tentang pelajaran trigonometri di kelas X yang mempelajari tentang konsep dasar perbandingan trigonometri↝ . Nahhh materi tersebut jangan dilupakan yaaa, sebab materi tersebut merupakan salah satu prasyarat untuk memahami modul ini. Yuk ah gak usah takut dan tidak bisa dengan trigonometri, kita belajar bertahap dan yakin pasti bisa…

1. Rumus untuk $\cos(\alpha+\beta)$ dan $\cos(\alpha-\beta)$

Pembuktian rumus $\cos(\alpha+\beta)=\cos\alpha \cos\beta -\sin\alpha \sin\beta $

Mari kita buktikan kedua rumus tersebut. Ada 2 cara untuk membuktikannya

Cara 1: Dengan lingkaran satuan, cari jarak dua titik

Perhatikan lingkaran satuan dan 3 buah juring yang masing-masing sudutnya $\alpha$, $\beta$, dan $-\beta$. 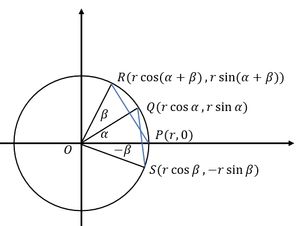Gambar di atas adalah lingkaran satuan yang berpusat di O dan berjari-jari $r$. Perhatikan dua segitiga yaitu $\vartriangle POR$ dan $\vartriangle SOQ$ dengan $\angle POR$ dan $\angle SOQ$ sehingga $PR=SQ$.

Dengan membuktikan $PR=SQ$, maka diperoleh $\cos(\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$ Dari gambar tersebut, diperoleh
$ OP=OQ=OR=OS = r$ Titik koordinat kutubnya yaitu titik $ P(r, 0)$,
titik $Q(r \cos \alpha, r \sin \alpha )$,
titik $R(r \cos(\alpha + \beta ), r \sin(\alpha + \beta ))$ , dan titik $ S(r \cos \beta , -r \sin \beta ) $.
Mengingat

1. Konsep jarak dua titik A($x_1,y_1$) dan B($x_2,y_2$) : $$ \begin{align*} AB &= \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 } \\ AB^2 &= (x_2-x_1)^2 + (y_2-y_1)^2 \end{align*} $$
2. Identitas trigonometri : $ \sin ^2 A + \cos ^2 A = 1 $

Pembuktian rumus $\sin(\alpha+\beta)=\sin\alpha \cos\beta -\cos\alpha \sin\beta $
Mencari Jarak PR :
$ P(r, 0)$ dan $ R (r \cos(\alpha + \beta ) , r \sin(\alpha + \beta )) $ dengan konsep jarak dua titik diatas $$ \begin{align*}PR^2 &= [r \cos(\alpha + \beta ) - r]^2 + [r \sin(\alpha + \beta ) - 0 ]^2 \\ &= [r \cos(\alpha + \beta ) - r]^2 + [r \sin(\alpha + \beta ) - 0 ]^2 \\ &= r^2 \cos ^2 (\alpha + \beta ) - 2r^2 \cos(\alpha + \beta ) + r^2 + r^2 \sin ^2 (\alpha + \beta ) \\ &= r^2 [\cos ^2 (\alpha + \beta ) + \sin ^2 (\alpha + \beta ) ]- 2r^2 \cos(\alpha + \beta ) + r^2 \\ &= r^2 [1 ]- 2r^2 \cos(\alpha + \beta ) + r^2\\ PR^2 &= 2r^2 - 2r^2 \cos(\alpha + \beta ) \end{align*} $$ **Mencari Jarak QS :**
$ Q(r \cos \beta , -r \sin \beta )$ dan $ S(r \cos \alpha, r \sin \alpha ) $ dengan konsep jarak dua titik diatas $$ \begin{align*}QS^2 &= [r \cos \alpha - r \cos \beta]^2 + [r \sin \alpha - ( -r \sin \beta ) ]^2 \\ &= [r \cos \alpha - r \cos \beta]^2 + [r \sin \alpha + r \sin \beta ]^2 \\ &= (r^2 \cos ^2 \alpha - 2r^2 \cos \alpha \cos \beta + r^2 \cos ^2 \beta ) + ( r^2 \sin ^2 \alpha + 2r^2 \sin \alpha \sin \beta + r^2 \sin ^2 \beta ) \\ &= r^2 (\cos ^2 \alpha + \sin ^2 \alpha ) + r^2 ( \cos ^2 \beta + \sin ^2 \beta) -2r^2 ( \cos \alpha \cos \beta - \sin \alpha \sin \beta ) \\ &= r^2 (1 ) + r^2 ( 1 ) -2r^2 ( \cos \alpha \cos \beta - \sin \alpha \sin \beta ) \\ QS^2 &= 2r^2 -2r^2 ( \cos \alpha \cos \beta - \sin \alpha \sin \beta ) \end{align*} $$ **Panjang PR sama dengan panjang QS** $$ \begin{align*}PR &= QS \\PR^2 &= QS^2 \\2r^2 - 2r^2 \cos(\alpha + \beta ) &= 2r^2 -2r^2 ( \cos \alpha \cos \beta - \sin \alpha \sin \beta ) \\ \cos(\alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{align*} $$ Sehingga Terbukti : $ \cos(\alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $

Pembuktian rumus $ \cos(\alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $

Rumus $\cos(\alpha-\beta)$ dapat diperoleh dengan sifat relasi sudut negatif yaitu $\cos(\alpha+(-\beta))$
Konsep sudut negatif : $ \sin (-A) = - \sin A$ dan $ \cos ( -A) = \cos A $
$$ \begin{align*} \cos(\alpha - \beta ) &= \cos(\alpha + (- \beta) ) \\ &= \cos \alpha \cos (-\beta) - \sin \alpha \sin (- \beta ) \\ &= \cos \alpha \cos \beta - \sin \alpha . (- \sin \beta) \\ &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{align*} $$ Sehingga terbukti : $ \cos(\alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $

Cara 2: Menggunakan Aturan Cosinus dan Jarak Dua Titik

Perhatikan gambar berikut,
Pada gambar, misalkan lingkaran satuan dengan jari-jari $r= 1$ dan pusat lingkaran O. Perhatikan $\triangle SOQ$, diperoleh titik koordinat kutubnya adalah titik S dan titik Q yaitu $ S(\cos \beta , -\sin \beta) $ dan $ Q(\cos \alpha , \sin \alpha ) $ serta OS = OQ = 1.
Ingat
Identitas trigonometri : $ \sin ^2 A + \cos ^2 A = 1 $
Selanjutnya mencari jarak titik S dan Q dengan rumus:
$$\begin{align*}SQ^2 &= (x_2-x_1)^2 + (y_2-y_1)^2 \\ SQ^2 &= (\cos \alpha - \cos \beta)^2 + (\sin \alpha - \sin \beta)^2 \\ &= (\cos ^2 \alpha - 2\cos \alpha \cos \beta + \cos ^2 \beta) + (\sin ^2 \alpha - 2\sin \alpha \sin \beta + \sin ^2 \beta) \\ &= ( \sin ^2 \alpha + \cos ^2 \alpha ) + (\sin ^2 \beta + \cos ^2 \beta ) - 2(\cos \alpha \cos \beta + \sin \alpha \sin b) \\ &= (1) + (1 ) - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) \\ SQ^2 &= 2 - 2(\cos \alpha \cos b + \sin a \sin b) \end{align*} $$ **Aturan cosinus pada segitiga POQ**
Perhatikan $\triangle SOQ$ berlaku aturan cosinus $SQ^2 = OS^2 + OQ^2 - 2.OS.OQ .\cos (\alpha-\beta)$ selanjutnya substitusi $ SQ^2 = 2 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) $ $$ \begin{align*} SQ^2 &= OS^2 + OQ^2 - 2.OS.OQ .\cos (\alpha-\beta)\\ SQ^2 &= 1^2 + 1^2 - 2.1.1 . \cos (\alpha-\beta) \\ 2 - 2 \cos (\alpha-\beta) &= SQ^2 \\ & \text{(substitusi } SQ^2 ) \\ 2 - 2 \cos (\alpha-\beta) &= 2 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)\\ \cos (\alpha-\beta) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{align*} $$
sehingga terbukti : $ \cos (\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $

Contoh Soal Trigonmetri Jumlah dan Selisih Dua Sudut Cosinus

1). Tentukan nilai dari $\cos 15^\circ$
Alternatif Penyelesaian
Gunakan rumus $\cos (a-b) = \cos a \cos b + \sin a \sin b$. $$\begin{align*} \cos 15^\circ & = \cos (45^\circ - 30^\circ) \\ & = \cos 45^\circ \cos 30^\circ + \sin 45^\circ \sin 30^\circ \\ & = \frac{1}{2}\sqrt{2} . \frac{1}{2}\sqrt{3} + \frac{1}{2}\sqrt{2} . \frac{1}{2} \\ & = \frac{1}{4}\sqrt{6}+ \frac{1}{4}\sqrt{2} \\ & = \frac{1}{4}\left( \sqrt{6} +\sqrt{2}\right ) \\ & = \frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3} + 1) \end{align*} $$ Jadi, nilai dari $\cos 105^\circ$ adalah $\frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3} + 1)$.

2). Tentukan nilai dari $\cos 105^\circ$
Alternatif Penyelesaian
Gunakan rumus $\cos (a+b) = \cos a \cos b - \sin a \sin b$. $$\begin{align*} \cos 105^\circ & = \cos (60^\circ + 45^\circ) \\ & = \cos 60^\circ \cos 45^\circ - \sin 60^\circ \sin 45^\circ \\ & = \frac{1}{2}. \frac{1}{2}\sqrt{2} - \frac{1}{2}\sqrt{3} . \frac{1}{2}\sqrt{2} \\ & = \frac{1}{4}\sqrt{2}- \frac{1}{4}\sqrt{6} \\ & = \frac{1}{4}\left( \sqrt{2} -\sqrt{6}\right ) \\ & = \frac{1}{4}\sqrt{2} (1-\frac{1}{2}\sqrt{3}) \end{align*} $$

3). Tentukan nilai dari $\cos 88^\circ \cos 58^\circ + \sin 88^\circ \sin 58^\circ$
Alternatif Penyelesaian
Gunakan rumus $ \cos a \cos b + \sin a \sin b=\cos (a-b)$. $$\begin{align*} \cos 88^\circ \cos 58^\circ + \sin 88^\circ \sin 58^\circ & = \cos (88^\circ-58^\circ)\\ &= \cos 30^\circ \\ &= \frac{1}{2}\sqrt{3}\end{align*} $$ jadi, nilai dari $\cos 88^\circ \cos 58^\circ + \sin 88^\circ \sin 58^\circ$ adalah $\frac{1}{2}\sqrt{3}$

4). Diketahui Diketahui $\cos x =\dfrac35$ dan $\cos y = \dfrac{12}{13}$ ($x$ dan $y$ sudut lancip). Tentukan nilai dari $\cos(x-y)$!
Alternatif Penyelesaian
Gunakan rumus $ \cos (x-y)=\cos x \cos y + \sin x \sin y$.
cos $x$ dan cos $y$ telah diketahui, sehingga kita perlu menentukan $\sin x$ dan $\sin y$ terlebih dahulu dengan menggunakan rumus identitas $\sin^2 x+\cos^2x=1$ atau bisa juga dengan menggambar segitiga.
Dari Identitas $\sin^2 x+\cos^2x=1$,

-) maka $\sin^2 x=1-\cos^2x$. $$\begin{align*}\sin^2 x&=1-\cos^2x\\ \sin x&=+\sqrt{1-\cos^2x} \text{ … }x \text { lancip, maka } \sin x \text{ positif}\\ &=+\sqrt{1-\left(\frac35\right)^2}\\ &=+\sqrt{1-\frac{9}{25}}\\ &=\sqrt{\frac{25}{25}-\frac{9}{25}}=\sqrt{\frac{16}{25}}\\ \sin x&=\frac{4}{5}\end{align*}$$

-) selanjutnya $\sin^2 y=1-\cos^2y$. $$\begin{align*}\sin^2 y&=1-\cos^2y\\ \sin y&=+\sqrt{1-\cos^2y} \text{ … }y \text { lancip, maka } \sin y \text{ positif}\\ &=+\sqrt{1-\left(\frac{12}{13}\right)^2}\\ &=+\sqrt{1-\frac{144}{169}}\\ &=\sqrt{\frac{169}{169}-\frac{144}{169}}=\sqrt{\frac{25}{169}}\\ \sin x&=\frac{5}{13}\end{align*}$$

-) mengitung nilai $\cos (x-y)$ $$\begin{align*} \cos (x-y)&=\cos x \cos y + \sin x \sin y \\ &=\left(\frac{3}{5}\right)\left(\frac{12}{13}\right) + \left(\frac{4}{5}\right)\left(\frac{5}{13}\right) \\ &=\frac{36}{65} + \frac{20}{65} \\ &=\frac{56}{65} \end{align*}$$ Jadi, nilai dari $\cos(x-y)=\dfrac{56}{65}$

2. Rumus untuk $\sin(\alpha+\beta)$ dan $\sin(\alpha-\beta)$

Untuk membuktikan rumus $sin(\alpha+\beta)$ dan $sin(\alpha-\beta)$diatas kita cukup menggunakan sifat relasi sudut di kuadran I dari pembuktian $cos(\alpha+\beta)$ diatas. Sebenarnya ada cara lain yaitu dengan menggunakan luas segitiga. Namun, kali ini kita gunakan relasi sudut di kuadran I saja.

Ingat relasi sudut $\sin A=\cos (90^\circ-A)$

Bukti rumus $ \sin(\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $

$$ \begin{align*} \sin ( \alpha + \beta ) &= \cos [90^\circ - ( \alpha + \beta )] \\ &= \cos [90^\circ - \alpha - \beta ] \\ &= \cos [(90^\circ - \alpha) - \beta ] \\ &= \cos (90^\circ - \alpha) \cos \beta + \sin (90^\circ - \alpha) \sin \beta \\ \sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{align*} $$ Jadi, terbukti : $ \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $

Bukti rumus $ \sin(\alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $

$$ \begin{align*} \sin ( \alpha - \beta ) &= \sin ( \alpha +(-\beta))\\ &= \sin \alpha \cos (-\beta ) + \cos \alpha \sin ( - \beta ) \\ &= \sin \alpha \cos \beta + \cos \alpha . (- \sin \beta ) \\ \sin ( \alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{align*} $$ Jadi, terbukti : $ \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $

Contoh Soal Trigonmetri Jumlah dan Selisih Dua Sudut Sinus

1). Tentukan nilai dari $\sin 15^\circ$
Alternatif Penyelesaian
Gunakan rumus $\sin (a-b) = \sin a \cos b + \cos a \sin b$. $$\begin{align*} \sin 15^\circ & = \sin (45^\circ - 30^\circ) \\ & = \sin 45^\circ \cos 30^\circ - \cos 45^\circ \sin 30^\circ \\ & = \frac{1}{2}\sqrt{2} . \frac{1}{2}\sqrt{3} + \frac{1}{2}\sqrt{2} . \frac{1}{2} \\ & = \frac{1}{4}\sqrt{6}- \frac{1}{4}\sqrt{2} \\ & = \frac{1}{4}\left( \sqrt{6} -\sqrt{2}\right ) \\ & = \frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3} - 1) \end{align*} $$ Jadi, nilai dari $\sin 15^\circ$ adalah $\frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3} - 1)$

2). Tentukan nilai dari $\sin 75^\circ$
Alternatif Penyelesaian
Gunakan rumus $\sin (a+b) = \sin a \cos b + \cos a \sin b$. $$\begin{align*} \sin 75^\circ & = \sin (45^\circ + 30^\circ) \\ & = \sin 45^\circ \cos 30^\circ + \cos 45^\circ \sin 30^\circ \\ & = \frac{1}{2}\sqrt{2}. \frac{1}{2}\sqrt{3} + \frac{1}{2}\sqrt{2} . \frac{1}{2} \\ & = \frac{1}{4}\sqrt{6}+ \frac{1}{4}\sqrt{2} \\ & = \frac{1}{4}\left( \sqrt{6} +\sqrt{2}\right ) \\ & = \frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3}+1) \end{align*} $$ Jadi, nilai dari $\sin 75^\circ$ adalah $\frac{1}{4}\sqrt{2} (\frac{1}{2}\sqrt{3}+1)$

3). Tentukan nilai dari $\sin 64^\circ \cos 56^\circ + \cos 64^\circ \sin 41^\circ$
Alternatif Penyelesaian
Gunakan rumus $ \sin a \cos b + \cos a \sin b=\sin (a+b)$. $$\begin{align*} \sin 64^\circ \cos 56^\circ + \cos 64^\circ \sin 56^\circ & = \sin (64^\circ+56^\circ)\\ &= \sin 120^\circ=\sin 30^\circ \\ &= \frac{1}{2}\end{align*} $$ Jadi, nilai dari nilai dari $\sin 64^\circ \cos 56^\circ + \cos 64^\circ \sin 41^\circ$ adalah $\dfrac{1}{2}$.

4). Diketahui Diketahui $\sin p =\dfrac35$ dan $\cos q = \dfrac{12}{13}$ ($p$ di kuadran III dan $q$ sudut lancip). Tentukan nilai dari $\sin(p+q)$!
Alternatif Penyelesaian
Gunakan rumus $ \sin (p+q)=\sin p \cos q + \cos p \sin q$.
sin $p$ dan cos $q$ telah diketahui, sehingga kita perlu menentukan $\cos p$ dan $\sin q$ terlebih dahulu dengan menggunakan rumus identitas $\sin^2 p+\cos^2q=1$ atau bisa juga dengan menggambar segitiga.
Dari Identitas $\sin^2 p+\cos^2q=1$,

*) maka $\cos^2 p=1-\sin^2q$.

$$\begin{align*}\cos^2 p&=1-\sin^2p\\ \cos p&=-\sqrt{1-\sin^2p} \text{ … }p \text { dikuadran III, maka } \cos p \text{ negatif}\\ &=-\sqrt{1-\left(\frac35\right)^2}\\ &=-\sqrt{1-\frac{9}{25}}\\ &=-\sqrt{\frac{25}{25}-\frac{9}{25}}=-\sqrt{\frac{16}{25}}\\ \cos p&=-\frac{4}{5}\end{align*}$$

*) selanjutnya $\sin^2 q=1-\cos^2q$.

$$\begin{align*}\sin^2 q&=1-\cos^2q\\ \sin q&=+\sqrt{1-\cos^2q} \text{ … }q \text { lancip, maka } \sin q \text{ positif}\\ &=+\sqrt{1-\left(\frac{12}{13}\right)^2}\\ &=+\sqrt{1-\frac{144}{169}}\\ &=\sqrt{\frac{169}{169}-\frac{144}{169}}=\sqrt{\frac{25}{169}}\\ \sin q&=\frac{5}{13}\end{align*}$$

*) mengitung nilai $\sin (p+q)$

$$\begin{align*} \sin (x+y)&=\sin p \cos q + \cos p \sin q \\ &=\left(\frac{3}{5}\right)\left(\frac{12}{13}\right) + \left(-\frac{4}{5}\right)\left(\frac{5}{13}\right) \\ &=\frac{36}{65} - \frac{20}{65} \\ &=\frac{16}{65} \end{align*}$$ Jadi, nilai dari $\sin(p+q)=\dfrac{16}{65}$

3. Rumus untuk $\tan(\alpha+\beta)$ dan $\tan(\alpha-\beta)$

Untuk membuktikan rumus $\tan(\alpha+\beta)$ dan $\tan(\alpha-\beta)$ diatas kita gunakan rumus trigonometri jumlah dua sudut $cos(\alpha+\beta)$ dan $cos(\alpha+\beta)$. Selain itu, kita juga menggunakan rumus identitas trigonometri $\tan A=\dfrac{\sin A}{\cos B}$.

Bukti rumus $ \tan ( \alpha + \beta ) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } $

$$\begin{align*} \tan ( \alpha + \beta ) & = \frac{ \sin ( \alpha + \beta ) }{\cos ( \alpha + \beta )} \\ & = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} \\ & = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} . \frac{\frac{1}{\cos \alpha \cos \beta}}{\frac{1}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\frac{\cos \alpha \cos \beta - \sin \alpha \sin \beta}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha \cos \beta }{\cos \alpha \cos \beta} + \frac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\frac{ \cos \alpha \cos \beta}{\cos \alpha \cos \beta} - \frac{ \sin \alpha \sin \beta}{\cos \alpha \cos \beta}} \\ & = \frac{\frac{\sin \alpha }{\cos \alpha } + \frac{ \sin \beta}{ \cos \beta}}{1 - \frac{ \sin \alpha }{\cos \alpha }\frac{ \sin \beta}{ \cos \beta}} \\ \tan ( \alpha + \beta ) & = \frac{ \tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } \end{align*} $$

Terbukti bahwa $ \tan ( \alpha + \beta ) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } $

Bukti rumus $ \tan ( \alpha - \beta ) = \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta } $

Untuk membuktikannya kita gunakan sudut berelasi di kuadran IV atau sudut negatif. Ingat bahwa $\tan (-A)=-\tan A$. $$\begin{align*} \tan ( \alpha - \beta ) & = \tan ( \alpha + (- \beta )) \\ & = \frac{ \tan \alpha + \tan (-\beta )}{1 - \tan \alpha \tan (-\beta ) } \\ & = \frac{ \tan \alpha - \tan \beta }{1 - \tan \alpha . (- \tan \beta ) } \\ & = \frac{ \tan \alpha - \tan \beta }{1 + \tan \alpha \tan \beta } \end{align*} $$

Contoh Soal Trigonometri Jumlah dan Selisih Dua Sudut Tangen

1). Tanpa menggunakan kalkulator dan tabel trigonometri. Tentukan nilai dari $\tan 75^\circ$!
Alternatif Penyelesaian
Gunakan rumus $\tan (a+b) = \dfrac{\tan a + \tan b}{1-\tan a. \tan b}$. $$\begin{align*} \tan 75^\circ & = \tan ( 45^\circ + 30^\circ ) \\ & = \frac{ \tan 45^\circ + \tan 30^\circ}{1 - \tan 45^\circ \tan 30^\circ } \\ & = \frac{ 1 + \frac{1}{3} \sqrt{3} }{1 - 1.\frac{1}{3} \sqrt{3} } \\ & = \frac{ 1 + \frac{1}{3} \sqrt{3} }{1 - \frac{1}{3} \sqrt{3} } \times \frac{3}{3} \\ & = \frac{ 3 + \sqrt{3} }{3 - \sqrt{3} } \\ & = \frac{ 3 + \sqrt{3} }{3 - \sqrt{3} } \times \frac{ 3 + \sqrt{3} }{3 + \sqrt{3} } \\ & = \frac{ 9 + 6\sqrt{3} + 3 }{9 - 3 }\\& = \frac{ 12 + 6\sqrt{3} }{6 }\\ \tan 75^\circ & = 2 + \sqrt{3} \end{align*} $$ Jadi, nilai dari $\tan 75^\circ= 2+\sqrt{3}$.

2). Tentukan nilai dari $\tan 255^\circ$
Alternatif Penyelesaian
Gunakan rumus $\tan (a-b) = \dfrac{\tan a - \tan b}{1+\tan a. \tan b}$. $$\begin{align*} \tan 255^\circ &= \tan(300^\circ-45^\circ)\\ &= \frac{\tan 300^\circ - \tan 45^\circ}{1+\tan 300^\circ \tan 45^\circ}\\ &= \frac{-\tan 60^\circ - \tan 45^\circ}{1-\tan 60^\circ \tan 45^\circ}\\ &= \frac{-\sqrt{3} - 1}{1-\sqrt{3} \cdot 1}\\ &= \frac{-\sqrt{3}-1}{-\sqrt{3}+1}\times \frac{-1}{-1}\\ &= \frac{\sqrt{3}+1}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1}\\ &= \frac{3+2\sqrt{3}+1}{3-1}\\ &= \frac{4+2\sqrt{3}}{2}\\ &= 2+\sqrt{3} \end{align*} $$ Jadi, nilai dari $\tan 255^\circ= 2+\sqrt{3}$.

3). Diketahui Diketahui $\sin p =\dfrac35$ dan $\cos q = \dfrac{12}{13}$ ($p$ di kuadran I dan $q$ di kuadran IV). Tentukan nilai dari $\tan(p+q)$!
Alternatif Penyelesaian
Gunakan rumus $\tan (a+b) = \dfrac{\tan a+\tan b}{1-\tan a. \tan b}$.
sin $p$ dan cos $q$ telah diketahui, sehingga kita perlu menentukan $\tan p$ dan $\tan q$ terlebih dahulu dengan menggambar segitiga saja.

Ingat perbandingan trigonometri
$\sin p =\dfrac{depan}{miring}=\dfrac{de}{mi}$
$\cos p =\dfrac{samping}{miring}=\dfrac{sa}{mi}$
$\tan p =\dfrac{depan}{samping}=\dfrac{de}{sa}$
Untuk $\sin p =\dfrac35=\dfrac{de}{mi}$ maka depan 3 miring 5 dan nilai $\tan p$ positif karena di kuadran I.
Untuk $\cos p =\dfrac{12}{13}=\dfrac{sa}{mi}$ maka depan 3 miring 5 dan nilai $\tan q$ negatif karena di kuadran IV.
Lihat gambar!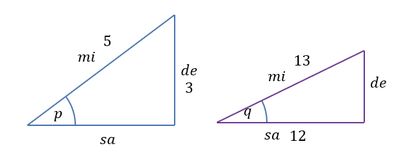

*) cari nilai $\tan p$ namun sebelumnya kita perlu mencari panjang samping dari segitiga dengan sudut $p$ dengan pythagoras.

$$sa=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$$ Sehingga nilai dari $\tan p=\dfrac{de}{sa}=\dfrac{3}{4}$.

*) cari nilai $\tan q$ namun sebelumnya kita perlu mencari panjang samping dari segitiga dengan sudut $q$ dengan pythagoras.

$$de=\sqrt{13^2-12^2}=\sqrt{169-144}=\sqrt{25}=5$$ Sehingga nilai dari $\tan q=-\dfrac{de}{sa}=-\dfrac{5}{12}$ (negatif karena di kuadran IV).

*) cari nilai $\tan (p+q)$.

$$\begin{align*} \tan (p+q) &= \frac{\tan p+\tan q}{1-\tan p. \tan q}\\ &=\frac{\frac{3}{4}+\left(-\frac{5}{12}\right)}{1-\frac{3}{4}.\left(-\frac{5}{12}\right)}\\ &=\frac{\frac{3}{4}-\frac{5}{12}}{1+\frac{15}{48}}\\ &=\frac{\frac{36}{48}-\frac{20}{48}}{\frac{48}{48}+\frac{15}{48}}\\ &=\frac{\frac{16}{48}}{\frac{63}{48}}\\ &=\frac{16}{63} \end{align*}$$ Jadi, nilai dari $\tan(p+q)=\dfrac{16}{63}$