Transformasi Geometri: Refleksi (Pencerminan) | Matematika SMA Kelas XI

Translasi atau pencerminan pada Transformasi Geometri merupakan materi matematika kelas xi, yuk simak pengertian, contoh soal, dan cara menentukan bayangannya berikut

Hai Sobat Sinmat! Pernahkah kamu berhadapan dengan cermin? Bayangan kamu di cermin adalah hasil dari sebuah transformasi matematika yang disebut refleksi. Seru kan? Setelah sebelumnya kita belajar Translasi↝ , Kali ini kita akan belajar Transformasi geometri, termasuk refleksi. Refleksi adalah salah satu konsep penting dalam geometri yang menggambarkan bagaimana suatu objek geometris dapat memantulkan atau mencerminkan dirinya terhadap suatu garis atau bidang tertentu.

Perhatikan ilustrasi berikut

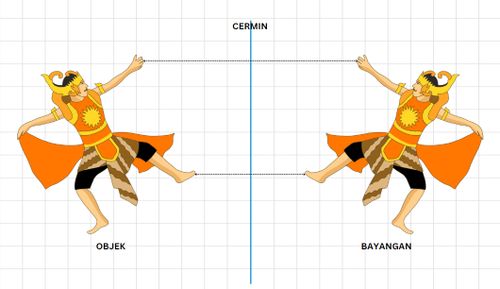
Gatotkaca berdiri di depan cermin dengan jarak 50 cm dan tinggi Gatotkaca adalah 160 cm. Bagaimana hasil refleksi Gatotkaca terhadap cermin? Bagaimana jarak bayangan Gatotkaca terhadap cermin ?

Sobat, jika kita lihat pada cermin hasil bayangan Gatotkaca berupa sosok Gatotkaca dengan bentuk, tinggi dan jarak bayangan sama namun arahnya saling berhadapan bukan?. Menurut kamu refleksi itu seperti apa nih, dan bagaimana sifanya? yuk baca selengkapnya.

Pengertian Refleksi pada Transformasi Geometri

Refleksi (pencerminan) adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan menggunakan sifat bayangan oleh suatu cermin. Refleksi disimbolkan dengan $𝑀_𝑎$ dengan $𝑎$ merupakan sumbu cermin.

Sifat-sifat Refleksi

Setelah memperhatikan ilustrasi pada gambar diatas kita peroleh nih sifat refleksi, yaitu

1. Jarak dari titik asal ke cermin sama dengan jarak cermin ke titik bayangan
2. Garis yang menghubungkan titik asal dengan titik bayangan tegak lurus terhadap cermin
3. Garis-garis yang terbentuk antara titik-titik asal dengan titik-titik bayangan akan saling sejajar

Selanjutnya, mari kita bahas jenis-jenis refleksi ya.

Jenis-jenis Refleksi pada Transformasi Geometri

1. Pencerminan terhadap sumbu $x$

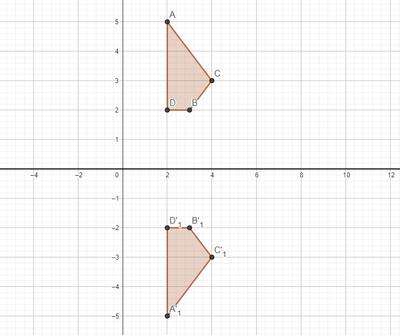Misalkan sembarang titik $A(x,y)$ dicerminkan terhadap sumbu $x$ akan menghasilkan bayangan $A'(x,-y)$. dapat kita tuliskan

$$A(x,y) \xrightarrow[]{M_{sbx}} A' (x, -y )$$ atau misal bayangannya $A'(x',y')$ dapat juga kita tuliskan dalam bentuk matrix transformasi Matriksnya : $M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ sebagai berikut $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ **Contoh**

1. Jika titik $𝐵(-2, 5)$ dicerminkan terhadap sumbu $𝑥$, tentukan bayangan titik B!

   Alternatif Penyelesaian ✍️

   $$B(x,y) \xrightarrow[]{M_{sbx}} B' (x', y' )$$ Hitung dengan matrix $$\begin{align*}\begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} -2 \\ 5 \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} -2\\ -5 \end{pmatrix}\end{align*}$$

   Jadi bayangannya adalah $B'(-2,-5)$.

2. Jika garis $𝑙: 3𝑥 − 2𝑦 − 5 = 0$ dicerminkan terhadap sumbu $𝑥$ maka hasil bayangan garis $𝑙$ adalah … Misal titik $𝐴(𝑥, 𝑦)$ memenuhi persamaan $3𝑥 − 2𝑦 − 5 = 0$ sehingga bayangan dari A adalah $A'(x',-y')$ (ubah tanda y menjadi kebalikannya) diperoleh $$x = x' \\ y=-y'$$ Substitusi $𝑥 = 𝑥'$ dan $𝑦 = −𝑦'$ ke persamaan garis 𝑙 $$\begin{align*}3x-2y-5=0\\ 3x'-2(-y')-5=0\\ 3x'+2y'-5=0 \end{align*}$$ Jadi, persamaan bayangan garis 𝑙 adalah $3𝑥 + 2𝑦 − 5 = 0$

2. Pencerminan terhadap sumbu $y$

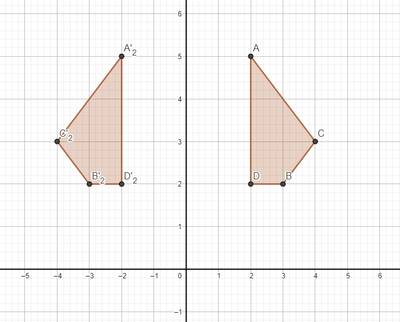Misalkan sembarang titik $A(x,y)$ dicerminkan terhadap sumbu $y$ akan menghasilkan bayangan $A'(-x,y)$. dapat kita tuliskan

$$A(x,y) \xrightarrow[]{M_{sby}} A' (x, -y )$$ atau misal bayangannya $A'(x',y')$ dapat juga kita tuliskan dalam bentuk matrix transformasi Matriksnya : $M = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$ sebagai berikut $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 &1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ **Contoh**

1. Tentukan bayangan titik A(1,2), B(3,-1) dan C(-4,-6) jika dicerminkan terhadap sumbu Y!

   Alternatif Penyelesaian ✍️

   • Untuk soal ini kita kerjakan sekaligus (bukan titik A atau B atau C sendiri-sendiri). caranya dengan menggunakan perkalian matriks $M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$
   • Bayangan titik A(1,2), B(3,-1) dan C(-4,-6) secara serentak : $$\begin{align*} \text{ bayangan } & = \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \times \text{ awal} \\ \begin{pmatrix}A' & B' & C' \end{pmatrix} & = \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \times \begin{pmatrix}1 & 3 & -4 \\ 2 & -1 & -6 \end{pmatrix} \\ & = \begin{pmatrix}1 & 3 & -4 \\ -2 & 1 & 6 \end{pmatrix} \end{align*}$$ Jadi, Kita peroleh bayangan masing-masing adalah $A' (1,-2), B' (3,1)$ dan $C' (-4,6)$.

2. Jika garis $𝑙: 2𝑥 − 3𝑦 + 12 = 0$ dicerminkan terhadap sumbu $Y$ maka hasil bayangan garis $𝑙$ adalah …

   Alternatif Penyelesaian ✍️

   • Matriks pencerminan terhadap sumbu Y : $M = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$
   • Menentukan hubungan $(x,y)$ dan $(x' , y' )$ : $$\begin{align*} \begin{pmatrix} x' \\ y' \end{pmatrix} & = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\\ \begin{pmatrix} x' \\ y' \end{pmatrix} & = \begin{pmatrix} -x \\ y \end{pmatrix} \end{align*}$$ Kita peroleh : $$x' = -x \rightarrow x = -x' \\ y' = y \rightarrow y = y'$$
   • Substitusi bentuk $x = -x'$ dan $y = y'$ ke persamaan awalnya sehingga kita dapatkan persamaan bayangannya : $$\begin{align*} 2𝑥 − 3𝑦 + 12 = 0 \\ 2(-𝑥') − 3𝑦' + 12 = 0 \\ -2x'-3y'+12=0 \text{ (kali -1) }\\ 2x'+3y'-12=0 \end{align*}$$ sehingga bayangannya $2x'+3y'-12=0$ atau $2x+3y-12=0$.

   Jadi, persamaan bayangannya adalah $2x+3y-12=0$. 😄

3. Pencerminan terhadap titik asal $O(0,0)$

4. Pencerminan terhadap garis $x=a$

5. Pencerminan terhadap garis $y=b$

6. Pencerminan terhadap titik asal $P(a,b)$

7. Pencerminan terhadap $y=x$

8. Pencerminan terhadap garis $y=-x$

9. Pencerminan terhadap garis $y=mx+c$

dimana $m=\tan \theta$