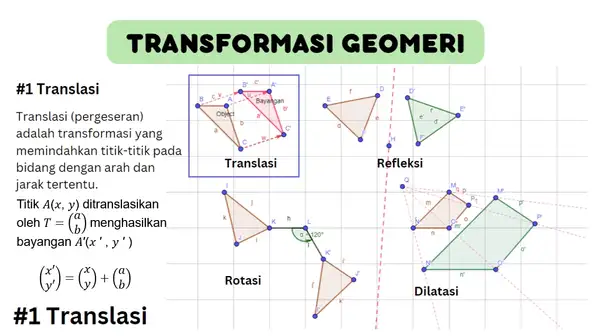
Translasi pada Transformasi Geometri merupakan materi matematika kelas xi yang harus kamu pelajari, yuk simak pengertian, contoh soal, dan cara menentukan bayangannya berikut

Sobat Sinmat! Tahu gak kalau banyak kegiatan atau kejadian dalam kehidupan sehari-hari kita yang terkait dengan transformasi geometri. Apa sih Transformasi Geometri itu? Transformasi geometri merupakan perubahan posisi dan ukuran dari suatu objek (titik, garis, kurva, bidang) dan dapat dinyatakan dalam gambar dan matriks. Transformasi Geometri biasanya akan kamu pelajari pada mata pelajaran matematika di kelas XI.

Beberapa hal yang akan kamu pelajari dalam transformasi geometri ini antara lain Translasi (Pergeseran), Refleksi (Pencerminan), Rotasi (Perputaran), dan Dilatasi (Penskalaan).

  1. Translasi merupakan transformasi yang memindahkan titik-titik pada bidang dengan arah dan jarak yang sama.
  2. Refleksi merupakan transformasi yang memindahkan tiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang akan dipindahkan. Bidang pencerminan dalam geometri terdiri atas sumbu X, sumbu Y, garis $𝑦 = mπ‘₯$, garis $𝑦 = βˆ’mπ‘₯$, garis $π‘₯ = π‘Ž$, garis $𝑦 = 𝑏$ dan terhadap titik pusat yaitu titik O (0,0).
  3. Rotasi merupakan transformasi yang memindahkan setiap titik oleh besar sudut dan pusat rotasi. Jika rotasi searah dengan jarum jam maka besar sudut negatif. Jika rotasi berlawanan dengan arah jarum jam maka besar sudut positif. Pusat rotasi terdiri atas titik asal yaitu O(0,0) dan titik tertentu yaitu P(a,b).
  4. Dilatasi merupakan transformasi ukuran atau skala suatu bangun geometri (pengecilan/pembesaran) tetapi tidak mengubah bentuk bangun tersebut. Dilatasi ditentukan oleh pusat dan faktor skala.

Yuk, kita bahas dulu dari translasi!

Pengertian Translasi pada Transformasi Geometri

Translasi memiliki makna pergeseran atau perpindahan. Translasi pada transformasi geometri adalah perpindahan dengan cara menggeser suatu benda (biasanya berupa titik, kurva, bangun datar, dan lainnya) menurut jarak dan arah tertentu. Misalkan, kita ingin memindahkan suatu titik dari posisi A ke posisi B, terjadi pergeseran sejauh $ a $ satuan arah horizontal dan sejauh $ b $ satuan arah vertikal. Sehingga transformasi untuk jenis translasi dapat kita tuliskan dalam bentuk matriks : $ T = \left( \begin{matrix} a \\ b \end{matrix} \right) $ .

Untuk mempermudah memahami konsep translasi kita bisa menggunakan pendekatan bidang Cartesius. Kita dapat mengasumsikan untuk pergeseran ke kanan pada bidang cartesius merupakan sumbu X positif, pergeseran ke kiri merupakan sumbu X negatif, pergeseran ke atas merupakan sumbu Y positif dan pergeseran ke bawah merupakan sumbu Y negatif.

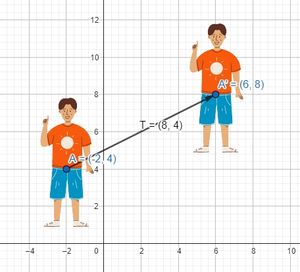
Perhatikan Ilustrasi Berikut! Ilustrasi Translasi

Misalkan Trawan ingin pergi ke suatu tempat dari titik awal A(-2,4). Trawan berjalan 8 satuan ke arah timur dan berjalan 4 satuan ke arah utara. Dapatkah kamu menentukan titik akhir dari Trawan?

Jika kita lihat bidang Cartesius berada pada koordinat titik awal Trawan adalah (-2,4). selanjutnya Trawan berjalan ke arah timur 8 satuan artinya posisi Trawan bergeser 8 satuan ke kanan dari posisi awal pada bidang Cartesius. Selanjutnya Trawan berjalan lagi ke arah utara sejauh 4 satuan artinya posisi Trawan bergeser 4 satuan ke atas. Jika kita melihat pada bidang Cartesius pada titik akhir posisi Trawan berada pada koordinat (6, 8). Hal ini berarti $$ \begin{pmatrix} -2 \\ 4 \end{pmatrix} + \begin{pmatrix} 8 \\ 4 \end{pmatrix} = \begin{pmatrix} 6 \\ 8 \end{pmatrix} $$

Jadi, posisi aKhir Trawan terletak pada koordinat (βˆ’4, βˆ’3)

Agar lebih mudah, berikut cara menentukan bayangan dari proses translasi pada Transformasi Geometri.

Rumus Perhitungan Translasi (Cara Menentukan Bayangan dari Transformasi Translasi)

Translasi (pergeseran) adalah transformasi yang memindahkan titik-titik pada bidang dengan arah dan jarak tertentu.

Misalkan sembarang titik $A(x,y) $ ditranslasikan oleh matriks translasi $ T = \begin{pmatrix} a \\ b \end{pmatrix} $, maka kita peroleh bayangannya yaitu $ A^\prime (x^\prime , y^\prime ) $, dapat kita tuliskan : $$ A(x,y) \xrightarrow[]{T = \begin{pmatrix} a \\ b \end{pmatrix}} A^\prime (x^\prime, y^\prime ) $$

Cara Penghitungannya : $$ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} a \\ b \end{pmatrix} $$

Sehingga kalau kita operasikan menjadi : $$ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} x + a \\ y + b \end{pmatrix} $$

$ T = \begin{pmatrix}π‘Ž\\𝑏 \end{pmatrix} $ disebut komponen translasi, π‘Ž merupakan pergeseran secara horizontal dan 𝑏merupakan pergeseran secara vertikal.

Titik 𝐴′ disebut bayangan titik 𝐴 yang telah ditranformasi.

Contoh Soal Translasi

Contoh 1

Tentukan bayangan titik A(3,-4) jika ditranslasikan oleh matriks $ T=\left( \begin{matrix} -1 \\ 2 \end{matrix} \right) $

Alternatif Penyelesaian ✍️

Menentukan bayangan titik $A(3,-4)$ : $$ \begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} a \\ b \end{pmatrix} \\ &= \begin{pmatrix} 3 \\ -4 \end{pmatrix}+ \begin{pmatrix} -1 \\ 2 \end{pmatrix} \\ &= \begin{pmatrix} 3 +(-1)\\ -4+2 \end{pmatrix} \\ &= \begin{pmatrix} 4\\ -2 \end{pmatrix} \end{align*} $$ Jadi, bayangan titik A adalah $ A^\prime (4,-2) $ πŸ˜„

Contoh 2

Tentukan bayangan kurva parabola $ 3x+2y=8 $ jika ditranslasikan oleh $T = \begin{pmatrix} -4 \ 1 \end{pmatrix} $!

Alternatif Penyelesaian ✍️

  • Karena persamaan atau fungsi ditransformasi, maka yang kita transformasikan adalah titik $(x,y)$, setelah itu kita ubah menjadi dalam bentuk $x^\prime $ dan $ y^\prime $.
  • Proses translasinya : $$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} a \\ b \end{pmatrix} \\ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} -4 \\ 1 \end{pmatrix} \end{align*} $$
  • rubah menjadi $x=..$ dan $y=…$ (pindahkan berdasar kesamaan matriks) $$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} - \begin{pmatrix} -4 \\ 1 \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x^\prime + 4 \\ y^\prime -1 \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix} \end{align*} $$ Kita peroleh : $ x = x^\prime + 4 , $ dan $ y = y^\prime - 1 $. bentuk inilah yang akan kita substitusikan ke persamaan awal $3x+2y=8$ sehingga kita peroleh persamaan bayangannya.
  • Substitusikan bentuk $ x = x^\prime + 4 , $ dan $ y = y^\prime - 1 $ ke persamaan awal $$ \begin{align*} 3x+2y&=8 \\ 3(x^\prime+4)+2(y^\prime-1)&=8 \\ 3x^\prime+12+2y^\prime-2&=8 \\ 3x^\prime+2y^\prime+10&=8 \\ 3x^\prime+2y^\prime&=-2 \end{align*} $$ Sehingga kita peroleh persamaan bayangannya yaitu $ 3x^\prime+2y^\prime=-2$ Jadi, persamaan bayangannya adalah $ 3x+2y=-2 $ πŸ˜„

Latihan Soal Translasi

Untuk memperdalam pengetahuanmu, silakan kerjakan soal latihan berikut!

  1. Tentukan bayangan titik $𝐴(3, 5)$ oleh translasi $𝑇 \begin{pmatrix}βˆ’2\\4\end{pmatrix}$!
  2. Garis $𝑙 ∢ 2π‘₯ βˆ’ 3𝑦 + 12 = 0$ ditranslasikan oleh $𝑇 \begin{pmatrix}1\\-2\end{pmatrix}$. Tentukan persamaan hasil translasi garis 𝑙 oleh T!