Menggambar sketsa grafik fungsi eksponen dapat dilakukan dengan langkah-langkah berikut
Daftar Isi
Grafik Fungsi Eksponen
Menggambar sketsa grafik fungsi eksponen dapat dilakukan dengan langkah-langkah berikut
- Menentukan titik-titik bantu dengan membuat daftar atau tabel yang menunjukkan hubungan antara nilai-nilai x dengan nilai-nilai $y=f(x)=k.{{a}^{x}}$ .
- Titik-titik dengan koordinat (x, y) yang diperoleh digambarkan pada bidang kartesius, kemudian dihubungkan dengan kurva mulus, sehingga diperoleh grafik fungsi eksponen $y=f(x)=k.{{a}^{x}}$
Untuk lebih jelasnya, perhatikan contoh berikut.
Contoh 1
Lukislah grafik fungsi $f(x)={{2}^{x}}$ untuk x bilangan real
penyelesaian
Menentukan titik koordinat dengan membuat tabel
| $x$ | $y=f(x)={{2}^{x}}$ | (x,y) |
|---|---|---|
| -3 | $\frac{1}{8}$ | $\left( -3,\frac{1}{8} \right)$ |
| -2 | $\frac{1}{4}$ | $\left( -2,\frac{1}{4} \right)$ |
| -1 | $\frac{1}{2}$ | $\left( -1,\frac{1}{2} \right)$ |
| 0 | 1 | (0,1) |
| 1 | 2 | (1,2) |
| 2 | 4 | (2,4) |
| 3 | 8 | (3,8) |
Tabel 2. Nilai fungsi $f(x)={{2}^{x}}$
Menggambar pada bidang kartesius
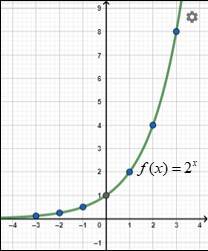Gambar 1. Grafik fungsi $f(x)={{2}^{x}}$
Contoh 2
Lukislah grafik fungsi $g(x)={{\left( \frac{1}{2} \right)}^{x}}$ untuk x bilangan real
Penyelesaian
| $x$ | $y=g(x)={{\left( \frac{1}{2} \right)}^{x}}$ | (x,y) |
|---|---|---|
| -3 | 8 | (-3,8) |
| -2 | 4 | (-2,4) |
| -1 | 2 | (-1,2) |
| 0 | 1 | (0,1) |
| 1 | $\frac{1}{2}$ | (1,1/2) |
| 2 | $\frac{1}{4}$ | (2,1/4) |
| 3 | $\frac{1}{8}$ | (3,1/8) |
Tabel 3. Nilai fungsi $g(x)={{\left( \frac{1}{2} \right)}^{x}}$
Menggambar pada bidang kartesius
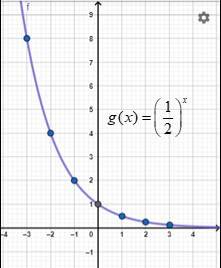Gambar 2. Grafik fungsi $g(x)={{\left( \frac{1}{2} \right)}^{x}}$
Perhatikan kedua contoh jika digabungkan.
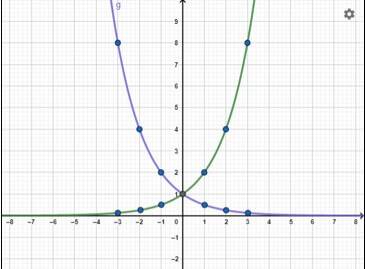Gambar 3. Grafik fungsi $f(x)={{2}^{x}}$dan$g(x)={{\left( \frac{1}{2} \right)}^{x}}$
Dengan memperhatikan gambar di atas terlihat bahwa:
- Domain kedua fungsi adalah himpunan semua bilangan real, ${{D}_{f}}\text{=}{x|x\in R}$ atau (-∞, ∞).
- Rangenya berupa himpunan semua bilangan real positif, ${{R}_{f}}\text{=}{y|y>0,y\in R}$ atau (0, ∞).
- Kedua grafik melalui titik (0, 1).
- Kurva mempunyai asimtot datar yaitu garis yang didekati fungsi tapi tidak akan berpotongan dengan fungsi, sumbu X (garis y = 0).
- Kedua grafik simetris terhadap sumbu Y
- Grafik $f(x)={{2}^{x}}$ merupakan grafik yang monoton naik, sedangkan grafik $g(x)={{\left( \frac{1}{2} \right)}^{x}}$ merupakan grafik yang monoton turun, dan keduanya berada di atas sumbu X (nilai fungsi senantiasa positif).
Dari grafik di atas, dapat disimpulkan bahwa fungsi $f:x\to {{a}^{x}}$, untuk $a>1$ adalah fungsi naik dan untuk $0<a<1$ adalah fungsi turun. Karena range dari 𝑓 adalah bilangan positif dan ${{a}^{0}}=1$, maka grafik fungsi $f:x\to {{a}^{x}}$ untuk $a>1$ dan $0<a<1$ terletak di atas sumbu 𝑥 dan melalui titik (0, 1).